uni/second/semester1/logseq-stuff/pages/Combinatorial Proofs.md

• #MA284 - Discrete Mathematics
• Previous Topic: Binomial Coefficients
• Next Topic: Stars & Bars
• Relevant Slides:

• Pascal's Triangle

  • Pascal's Identity: A recurrence relation for \binom{n}{k}:
    • \binom{n}{k} = \binom{n-1}{k-1} + \binom{n-1}{k}
  • In the previous topic, we "proved" that \binom{n}{k} = \frac{n!}{(n-k)!k!} by counting P(n,k) in two different ways.
    • This is a classic example of a Combinatorial Proof, where we establish a formula by counting something in 2 different ways.
  • 
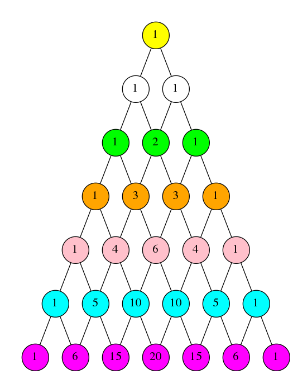
  • Binomial coefficients have many important properties. Looking at their arrangement in Pascal's Triangle, we can spot some:
    • (i) For all n, \binom{n}{0} = \binom{n}{n} = 1.
    • (ii) \displaystyle\sum^{n}_{i=0} \binom{n}{i}= 2^n
    • (iii) \binom{n}{k} = \binom{n-1}{k-1} + \binom{n-1}{k} (Pascal's Identity).
    • (iv) \binom{n}{k} = \binom{n}{n-k}

• Algebraic & Combinatorial Proofs

  • Proofs of identities involving Binomial Coefficients can be classified as:
    • Algebraic: If they rely mainly on the formula for binomial coefficients.

      • 
        \binom{n}{k} = \frac{n!}{k!(n-k)!}
        \newline
        \therefore \binom{n}{k} = \frac{n!}{(n-k)!(n-(n-k))!} = \frac{n!}{(n-k)!k!} = \binom{n}{k}
        

    • Combinatorial: If they involve counting a set in two different ways.
      • Let A be a set of size n.
      • \binom{n}{k} = number of subsets of A of cardinality k, but for each such subset there is a one-to-one correspondence with a subset of size n-k.
      • i.e., \binom{n}{n-k} = \binom{n}{k},

  • Algebraic Proof of Pascal's Triangle Recurrence Relation

    • \binom{n}{k} = \frac{n!}{k!(n-k)!} \newline \newline
    • \binom{n-1}{k-1} + \binom{n-1}{k} = \frac{(n-1)!}{(k-1)!(n-k)!} + \frac{(n-1)!}{k!(n-k-1)!}
    • = \frac{k(n-1)!}{k(k-1)!(n-k)!} + \frac{(n-1)!(n-k)}{k!(n-k-1)!(n-k)}
    • = \frac{k(n-1)!+(n-k)(n-1)!}{k!(n-k)!}
    • = \frac{(n-1)!(k+n-k)}{k!(n-k)!} = \frac{n!}{k!(n-k)!} = \binom{n}{k}

• Example:

  • Let A be a set with n elements.
  • Then, the total number of subsets of A can be counted as follows:
    • Generic subset: An element is either in it or not
    • For each of n elements, there are 2 choices: in or not in.
    • By Multiplicative principle, 2 \times 2 \times ... \times 2 such subsets [2^n = |P(n)|].
    • Number of subsets with:
      • 0

• How Combinatorial Proofs Work

  • Which are better: Algebraic or Combinatorial proofs?

    • When we first study discrete mathematics, algebraic proofs may seem to be the easiest: they rely only using some standard formulae, and don't require any deeper insight. They are also more "familiar".
    • However:
      • Often, algebraic proofs are quite tricky.
      • Usually, algebraic proofs give no insight as to why a fact is true.

  • Example

    • We wish to show that:
      • {\binom{n}{0}}^2 + {\binom{n}{1}}^2 + {\binom{n}{2}}^2 + ... + {\binom{n}{n}}^2 = \binom{2n}{n}
    • We note that \binom{2n}{n} is the total number of subsets of size n in a set with 2n elements.
    • Let A be a set with 2n elements, and label them A = \{a_1, a_2, ..., a_n, a_{n+1}, ..., a_{2n}\}.
    • Any subset of A with n elements has k elements from \{a_1 a_2, ..., a_n\} and n-k elements from t \{a_{n+1}, ..., a_{2n}\} where k ranges from 0 to n.
    • There are \displaystyle \binom{n}{k} \cdot \binom{n}{n-k} ways of choosing these n elements by the Multiplicative Principle.
    • So the total number of subsets with n elements is \displaystyle\sum^n_{k=0} \binom{n}{k} \binom{n}{n-k} and noting that \displaystyle \binom{n}{n-k} = \binom{n}{k} and the results follows.

  • Example

    • Using a combinatorial argument, or otherwise, prove that
      • k\binom{n}{k} = n\binom{n-1}{k-1}
    • Combinatorial Proof:
      • Suppose we have a panel of n players and we need to choose a team of k player with a distinguished player (e.g., the goalkeeper).
      • We count how many ways we can do this.
      • [A] Pick the team, then pick the goalie.
        • By the Multiplicative Principle, we can pick a team of k from n in \binom{n}{k} ways and have k ways then of choosing a keeper from this.
          • = k\binom{n}{k}
      • [B] Pick the goalie, then pick the remainder of the team.
        • We have n choices for the goalie. then choose k-1 from the n-1 remaining players.
        • By the Multiplicative Principle we have \displaystyle n\binom{n-1}{k-1} ways.
        • Result follows.

  • What is a "Combinatorial Proof" really? #card

    card-last-interval:: 9.28 card-repeats:: 3 card-ease-factor:: 2.32 card-next-schedule:: 2022-11-23T22:36:16.354Z card-last-reviewed:: 2022-11-14T16:36:16.354Z card-last-score:: 5
    • [1] These proofs involve finding two different ways to answer the same counting question.
    • [2] Then, we explain why the answer to the problem posed one way is A.
    • [3] Next, we explain why the answer to the problem posed the other way is B.
    • [4] Since A and B are answers to the same question, we have shown that it must be that A = B.