uni/year2/semester1/logseq-stuff/pages/Binomial Coefficients.md

• #MA284 - Discrete Mathematics
• Previous Topic: Principle of Inclusion-Exclusion
• Next Topic: Combinatorial Proofs
• Relevant Slides:

• Binary Strings & Lattice Paths

  • Binary Strings

    • A bit is a "binary digit", e.g., 1 or 0.
    • A bit string is a string (list) of bits, e.g., 1011010.
    • What is the length of a string? #card card-last-interval:: 31.36 card-repeats:: 4 card-ease-factor:: 2.8 card-next-schedule:: 2022-12-16T04:06:32.399Z card-last-reviewed:: 2022-11-14T20:06:32.399Z card-last-score:: 5
      • The length of the string is the number of bits.
        • An $n$-bit string has length n.
        • The set of all $n$-bit strings (for given n) is denoted B^n.
    • What is the weight of a string? #card card-last-interval:: 33.64 card-repeats:: 4 card-ease-factor:: 2.9 card-next-schedule:: 2022-12-21T00:50:01.239Z card-last-reviewed:: 2022-11-17T09:50:01.240Z card-last-score:: 5
      • The weight of the string is the number of 1s.
        • The set of all $n$-bit strings of weight k is denoted B^n_k.

  • Lattice Paths

    • What is a lattice? #card card-last-interval:: 19.01 card-repeats:: 4 card-ease-factor:: 2.18 card-next-schedule:: 2022-12-03T20:05:46.936Z card-last-reviewed:: 2022-11-14T20:05:46.936Z card-last-score:: 3
      • The (integer) lattice is the set of all points in the Cartesian plane for which both the x & y coordinates are integers.
    • What is a lattice path? #card card-last-interval:: 31.36 card-repeats:: 4 card-ease-factor:: 2.8 card-next-schedule:: 2022-12-16T04:11:02.220Z card-last-reviewed:: 2022-11-14T20:11:02.220Z card-last-score:: 5
      • A lattice path is the ^^shortest possible path^^ connecting two points on the lattice, moving only horizontally & vertically.
        • There can be multiple lattice paths, so long as they are of equally short length.
    • 
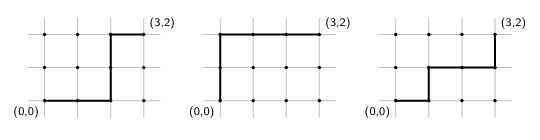
      • The number of lattice paths from (0,0) to (3,2) is the same as |B_3^5|.
      • The number of lattice paths from (0,0) to (3,2) is the same as the number from (0,0) to (2,2), plus the number from (0,0) to (3,1).

• Binomial Coefficients

  • What is the coefficient of say, x^3y^2 in (x+y)^5?
    • $$(x+y)^0=1 \newline (x+y)^1=x+y \newline (x+y)^2=x^2+2xy+y^2 \newline (x+y)^3=x^3+3x^2y+3xy^2+y^3 \newline (x+y)^4=x^4+4x^3y+6x^2y^2+4xy^3+y^4 \newline (x+y)^5=x^5+5x^4y+10x^3y^2+10x^2y^3+5xy^4+y^5

    • So, by doing a lot of multiplication, we have worked out that the coefficient of x^3y^2 is 10.
    • But, there is a more systematic way of answering this problem.
    • (x+y)^5=(x+y)(x+y)(x+y)(x+y)(x+y)
    • We can work out the coefficient of x^3y^2 in the expansion of (x+y)^5 by counting the number of ways we can choose 3 $x$s & 2 $y$s in
      • (x+y)(x+y)(x+y)(x+y)(x+y)
  • The numbers that occurred in all of our examples are called binomial coefficients, and are denoted
    • \binom{n}{k}
  • What are Binomial Coefficients? #card card-last-interval:: 9.88 card-repeats:: 3 card-ease-factor:: 2.32 card-next-schedule:: 2022-11-24T13:42:42.079Z card-last-reviewed:: 2022-11-14T16:42:42.079Z card-last-score:: 3
    • For each integer n \geq 0, and integer k such that 0 \leq k \leq n, there is a number \binom{n}{k}, read as "n choose $k$".
      • \binom{n}{k} = |B^n_k|, the number of $n$-bit strings of weight k.
      • \binom{n}{k} is the number of subsets of a set of size n, each with cardinality k.
      • \binom{n}{k} is the number of lattice paths of length n containing k steps to the right.
      • \binom{n}{k} is the coefficient of x^k y^{n-k} in the expansion of (x+y)^n.
      • \binom{n}{k} is the number of ways to select k objects from a total of n objects.
  • If we were to skip ahead, we would learn that there is a formula for \binom{n}{k} (that is, "n choose $k$") that is expressed in terms of factorials.
    • Recall that the factorial of a natural number n is:
      • n! = n \times (n-1) \times (n-2) \times (n-4) \times ... \times 2 \times 1
    • We will eventually learn that
      • \binom{n}{k} = \frac{n!}{k!(n-k)!}

    • However, the formula \displaystyle \binom{n}{k} = \frac{n!}{k!(n-k)!} is not very useful in practice.

• Pascal's Triangle

  • 
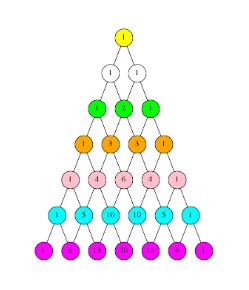
  • Earlier, we learned that if the set of all $n$-bit strings with weight k is written B^n_k, then
    • |b^n_k| = |B^{n-1}_{k-1}| + |B^{n-1}_k
  • Similarly, we find that:

    • Pascal's Identity: A recurrence relation for \binom{n}{k} #card

      card-last-interval:: -1 card-repeats:: 1 card-ease-factor:: 2.7 card-next-schedule:: 2022-11-18T00:00:00.000Z card-last-reviewed:: 2022-11-17T09:47:25.425Z card-last-score:: 1
      • \binom{n}{k} = \binom{n-1}{k-1} + \binom{n-1}{k}
    • This is often presented as Pascal's Triangle
    • 

• Permutations

  • What is a permutation? #card card-last-interval:: 33.64 card-repeats:: 4 card-ease-factor:: 2.9 card-next-schedule:: 2022-12-21T00:50:12.451Z card-last-reviewed:: 2022-11-17T09:50:12.452Z card-last-score:: 5
    • A permutation is an arrangement of objects. Changing the order of the objects gives a different permutation.
      • A permutation of a set must have the same cardinality as that set.
      • Important: order matters!

  • Number of Permutations

    • How many permutations are there of n objects? #card card-last-interval:: 31.36 card-repeats:: 4 card-ease-factor:: 2.8 card-next-schedule:: 2022-12-16T04:21:54.886Z card-last-reviewed:: 2022-11-14T20:21:54.886Z card-last-score:: 5
      • There are n! (i.e., n factorial) permutations of n (distinct) objects.
    • How many permutations are there of k objects from n? #card card-last-interval:: 31.36 card-repeats:: 4 card-ease-factor:: 2.8 card-next-schedule:: 2022-12-16T04:10:57.897Z card-last-reviewed:: 2022-11-14T20:10:57.897Z card-last-score:: 5
      • The number of permutations of k objects out of n, P(n,k) is
        • P(n,k) = \binom{n}{k} = n \times (n-1) \times ... \times (n - k + 1) = \frac{n!}{(n-k)!}

  • The Binomial Coefficient Formula

    • (1) We know that there are P(n,k) permutations of k objects out of n.
    • (2) We know that
      • P(n,k) = \frac{n!}{(n-k)!}
    • (3) Another way of making a permutation of k objects out of n is to
      • (a) Choose k from n without order. There \binom{n}{k} ways of doing this.
      • (b) Then count all the ways of ordering these k objects. There are k! ways of doing this.
      • (c) By the Multiplicative Principle,
        • P(n,k) = \binom{n}{k}k!
    • (4) So now we know that
      • \frac{n!}{(n-k)!} = \binom{n}{k}k!
    • (5) This gives the formula
      • \binom{n}{k} = \frac{n!}{(n-k)!k!}