uni/year2/semester1/logseq-stuff/pages/Matrices.md

• #MA284 - Discrete Mathematics
• Previous Topic: Trees
• Next Topic:
• Relevant Slides:
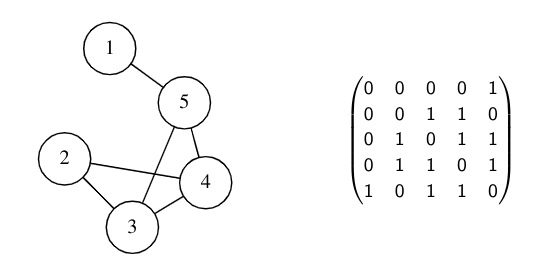
• In a practical setting, a graph must be stored in some computer-readable format.
  • One of the most common is an adjacency matrix.

• Adjacency Matrices

  • What is an adjacency matrix? #card
    • If the graph has n vertices, labelled \{1,2,\cdots, n\}, then the adjacency matrix is an m \times n binary matrix, A, with entries
      • $$a_{i,j} = \begin{cases} 1 & \text{vertex } i \text{ is adjacent to } j\ 0 & \text{otherwise.} \end{cases}$$
      • 

  • Properties of the Adjacency Matrix #card

    • The adjacency matrix of a graph is symmetric.
    • If B = A^k, then b_{i,j} is the number of paths of length k from vertex i to vertex j.
    • We can work out if a graph is connected by looking at the eigenvalues of A.
    • If the graphs G & H are isomorphic, and have adjacency matrices A_G & A_H, then there is a permutation matrix P, such that PA_GP^{-1}=A_H.
  • The adjacency matrix idea is easily extended to allow for multigraphs and pseudographs (graphs with loops).
    • For a multigraph, a_{i,j} is the number of edges joining vertices i & j.
    • For a pseudograph, a_{i,i} means that there is an edge from the vertex i to itself.

• Instance Matrices

  • Graphs can also be represented by an Incidence Matrix.
    • If the graph has v vertices, and e edges, then it is an v \times e binary matrix.
    • The rows represent vertices.
    • The columns represent edges.
    • If the matrix is B = (b_{i,j}) then b_{ik} = 1 means that the vertex i is incident to edge j.

• Distance Matrices

  • What is the eccentricity of a vertex?
    • The eccentricity of a vertex is the greatest distance between that vertex & any other vertex in the graph.
  • What is the radius of a graph? #card
    • The radius of a graph is the minimum eccentricity of any vertex.
  • What is the diameter of a graph?
    • The diameter of a graph is the maximum eccentricity of any vertex.
      • This is also the maximum entry in the distance matrix.