3.7 KiB
3.7 KiB
- #CT255 - Next Generation Technologies II
- Previous Topic: Social Engineering
- Next Topic: Block Ciphers & Stream Ciphers
- Relevant Slides:
-
Groups, Rings, & Fields
- In mathematics,
- a group is a set equipped with a binary operation that is associative, has an identity element, and is such that every element has an inverse, e.g.,
(\mathbb{Z}, +). - a ring is a set equipped with two binary operations satisfying properties analogous to those of addition & multiplication of integers, e.g.
(\mathbb{Z}, +, *). - a field is a set on which addition, subtraction, multiplication, & division are defined and behave as the corresponding operations on rational & real numbers do.
- a group is a set equipped with a binary operation that is associative, has an identity element, and is such that every element has an inverse, e.g.,
- In mathematics,
-
Diffie-Hellman Key Exchange
- What is the Diffie-Hellman Key Exchange? #card
card-last-interval:: 3.69
card-repeats:: 2
card-ease-factor:: 2.46
card-next-schedule:: 2022-11-22T10:36:42.441Z
card-last-reviewed:: 2022-11-18T18:36:42.441Z
card-last-score:: 5
- Diffie-Hellman provides secure key exchange between two partners.
- The negotiated key is subsequently used for private key encryption / authentication.
- It uses the multiplicative group of integers modulo
n(\mathbb{Z} / n \mathbb{Z})^x. - It is based on the difficulty of computing discrete logarithms over such groups, e.g.:
-
6^3 \text{ mod } 17 = 216 \text{ mod } 17 =12 \text{ (easy) } -
12 = 6 ^y \text{ mod } 17 ? \text{ hard }
-
- The core equation for the key exchange is
-
K = (A)^B \text{ mod } q
-
- Diffie-Hellman provides secure key exchange between two partners.
-
Diffie-Hellman: Global Public Elements
- Select a prime number
qand positive and a positive integera, wherea < qandais a primitive root ofq. - What is a primitive root? #card
card-last-interval:: 2.8
card-repeats:: 2
card-ease-factor:: 2.6
card-next-schedule:: 2022-11-24T08:08:29.696Z
card-last-reviewed:: 2022-11-21T13:08:29.697Z
card-last-score:: 5
ais a primitive root ofq, if numbersa \text{ mod } q, a^2 \text{ mod } q, \cdots , a^{q-1} \text{ mod } qare distinct integer values between1and(q-1)in some permutation, i.e., elements of(\mathbb{Z} / q \mathbb{Z})^x.- Example:
a = 3is a primitive root of(\mathbb{Z} / 5\mathbb{Z})^x,a=4is not: background-color:: green
- Select a prime number
-
Generation of Secret-Key
- Both users share a public prime number
qand primitive roota. - User A:
-
- Select secret number
XAwithXA < q. - Calculate public value
YA = a^{XA} \text{ mod } q(difficult to reverse). YAis sent to User B.
- Select secret number
-
- User B:
-
- Select secret number
XBwithXB < q. - Calculate public value
YB = a^{XB} \text{ mod } q(difficult to reverse). YBis sent to User A.
- Select secret number
-
- User A:
- User A owns
XAand receivesYB. - Generate secret key:
K = (YB)^{XA} \text{ mod } q.
- User A owns
- User B:
- User B owns
XBand receivesYA. - Generate secret key:
K = (YA)^{XB} \text{ mod } q.
- User B owns
- Both keys are identical.
- Both users share a public prime number
-
Diffie-Hellman in Practice
- The algorithm is used in tandem with a variety of secure network protocols.
- Provision of secure end-to-end connection.
- No endpoint authentication - you can't validate who you are talking to.
- Modulus
ptypically has a minimum length of 1024 bits.
- The algorithm is used in tandem with a variety of secure network protocols.
-
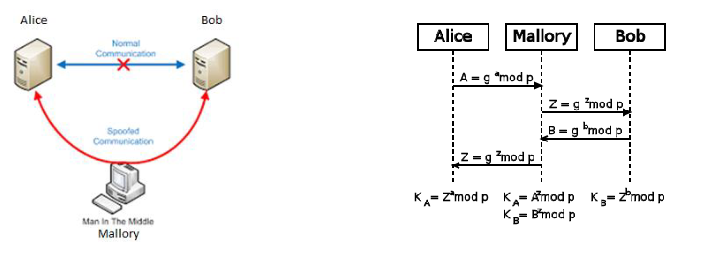
DH & Man-in-the-Middle (MitM) Attacks
- What is the Diffie-Hellman Key Exchange? #card
card-last-interval:: 3.69
card-repeats:: 2
card-ease-factor:: 2.46
card-next-schedule:: 2022-11-22T10:36:42.441Z
card-last-reviewed:: 2022-11-18T18:36:42.441Z
card-last-score:: 5