[CS4423]: Add assignment 1
This commit is contained in:
@ -0,0 +1,503 @@
|
||||
{
|
||||
"cells": [
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "e4dd8d87",
|
||||
"metadata": {
|
||||
"toc": true
|
||||
},
|
||||
"source": [
|
||||
"<h1>Table of Contents<span class=\"tocSkip\"></span></h1>\n",
|
||||
"<div class=\"toc\"><ul class=\"toc-item\"><li><ul class=\"toc-item\"><li><span><a href=\"#Collaboration-Policy\" data-toc-modified-id=\"Collaboration-Policy-0.1\"><span class=\"toc-item-num\">0.1 </span>Collaboration Policy</a></span></li><li><span><a href=\"#Instructions\" data-toc-modified-id=\"Instructions-0.2\"><span class=\"toc-item-num\">0.2 </span>Instructions</a></span></li><li><span><a href=\"#Preliminaries\" data-toc-modified-id=\"Preliminaries-0.3\"><span class=\"toc-item-num\">0.3 </span>Preliminaries</a></span></li><li><span><a href=\"#Usual-list-of-Python-modules\" data-toc-modified-id=\"Usual-list-of-Python-modules-0.4\"><span class=\"toc-item-num\">0.4 </span>Usual list of Python modules</a></span></li></ul></li><li><span><a href=\"#Q1:-Bipartite-Graphs\" data-toc-modified-id=\"Q1:-Bipartite-Graphs-1\"><span class=\"toc-item-num\">1 </span>Q1: Bipartite Graphs</a></span><ul class=\"toc-item\"><li><span><a href=\"#Define-and-draw-the-following-graph\" data-toc-modified-id=\"Define-and-draw-the-following-graph-1.1\"><span class=\"toc-item-num\">1.1 </span>Define and draw the following graph</a></span></li><li><span><a href=\"#Determine-if-$G_1$--is-bipartite.\" data-toc-modified-id=\"Determine-if-$G_1$--is-bipartite.-1.2\"><span class=\"toc-item-num\">1.2 </span>Determine if $G_1$ is bipartite.</a></span></li></ul></li><li><span><a href=\"#Q2:-A-Network-of-friends\" data-toc-modified-id=\"Q2:-A-Network-of-friends-2\"><span class=\"toc-item-num\">2 </span>Q2: A Network of friends</a></span><ul class=\"toc-item\"><li><span><a href=\"#Define-a-graph-in-networkx-that-represents-this---scenario.\" data-toc-modified-id=\"Define-a-graph-in-networkx-that-represents-this---scenario.-2.1\"><span class=\"toc-item-num\">2.1 </span>Define a graph in <code>networkx</code> that represents this scenario.</a></span></li><li><span><a href=\"#Verify-that-the-graph-has-the-correct-properties-by--displaying-the-diagonal-of-the-square-of-the-graphs-adjacency--matrix.\" data-toc-modified-id=\"Verify-that-the-graph-has-the-correct-properties-by--displaying-the-diagonal-of-the-square-of-the-graphs-adjacency--matrix.-2.2\"><span class=\"toc-item-num\">2.2 </span>Verify that the graph has the correct properties by displaying the diagonal of the square of the graphs adjacency matrix.</a></span></li></ul></li><li><span><a href=\"#Q3:-Isomorphic-graphs\" data-toc-modified-id=\"Q3:-Isomorphic-graphs-3\"><span class=\"toc-item-num\">3 </span>Q3: Isomorphic graphs</a></span><ul class=\"toc-item\"><li><span><a href=\"#Self-complementary-cycle-graph\" data-toc-modified-id=\"Self-complementary-cycle-graph-3.1\"><span class=\"toc-item-num\">3.1 </span>Self-complementary cycle graph</a></span></li><li><span><a href=\"#Graphs-that-are-isomorphic-to-their-line-graphs.\" data-toc-modified-id=\"Graphs-that-are-isomorphic-to-their-line-graphs.-3.2\"><span class=\"toc-item-num\">3.2 </span>Graphs that are isomorphic to their line graphs.</a></span></li></ul></li><li><span><a href=\"#Q4:-Bipartite-Graphs\" data-toc-modified-id=\"Q4:-Bipartite-Graphs-4\"><span class=\"toc-item-num\">4 </span>Q4: Bipartite Graphs</a></span></li><li><span><a href=\"#Q5:-Directed-Graphs\" data-toc-modified-id=\"Q5:-Directed-Graphs-5\"><span class=\"toc-item-num\">5 </span>Q5: Directed Graphs</a></span><ul class=\"toc-item\"><li><span><a href=\"#Construct-and-draw-a-digraph\" data-toc-modified-id=\"Construct-and-draw-a-digraph-5.1\"><span class=\"toc-item-num\">5.1 </span>Construct and draw a digraph</a></span></li><li><span><a href=\"#$G_5$-is-not-strongly-connected.\" data-toc-modified-id=\"$G_5$-is-not-strongly-connected.-5.2\"><span class=\"toc-item-num\">5.2 </span>$G_5$ is not strongly connected.</a></span></li><li><span><a href=\"#Permuting-the-adjacency-matrix.\" data-toc-modified-id=\"Permuting-the-adjacency-matrix.-5.3\"><span class=\"toc-item-num\">5.3 </span>Permuting the adjacency matrix.</a></span></li></ul></li></ul></div>"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "19989cc4",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# CS4423 Assignment 1: Solution Template\n",
|
||||
"\n",
|
||||
"This is a template for your solution to the `networkx` questions on Assignment 1. \n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "4fc2a5c6",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"### Collaboration Policy\n",
|
||||
"\n",
|
||||
"This is a homework assignment. You are welcome to collaborate with\n",
|
||||
"class-mates if you wish. Please note:\n",
|
||||
"* You may collaborate with at most two other people;\n",
|
||||
"* Each of you must submit your own copy of your work;\n",
|
||||
"* The file(s) you submit must contain a statement on the collaboration: who you collaborated with, and on what part of the assignment.\n",
|
||||
"* The use of any AI tools, such as ChatGPT or DeepSeek is prohibited, and will be subject to disciplinary procedures. \n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "a5bd0014",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"### Instructions \n",
|
||||
"\n",
|
||||
"This assignment involves a mix of questions, some of which require use of the `networkx` Python module, and some which you solve by hand. You can decide the best way to submit your work (e.g., do everything in Jupyter, or a combination of hand-written work and\n",
|
||||
"Jupyter notebook). However:\n",
|
||||
"* Any file you submit must include your name and ID number.\n",
|
||||
"* All files must be in PDF format. To convert your notebook to `pdf` the easiest method maybe to first export as 'html', then open that in a browser, and then print to pdf."
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "eb8aa930",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"### Preliminaries\n",
|
||||
"\n",
|
||||
"**Name:** Andrew Hayes\n",
|
||||
"\n",
|
||||
"**ID Number:** 213 \n",
|
||||
"*Place your collaboration statement here*"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "50688c85",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"### Usual list of Python modules"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"id": "d548d182",
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"import networkx as nx\n",
|
||||
"import numpy as np\n",
|
||||
"import matplotlib.pyplot as plt\n",
|
||||
"opts = { \"with_labels\": True, \"node_color\": 'y' } # show labels; yellow noodes"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "6d7af8b8",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"## Q1: Bipartite Graphs\n",
|
||||
"\n",
|
||||
"### Define and draw the following graph\n",
|
||||
"Let $G_1$ be the graph on the nodes $\\{0, 1, 2, 3, 4, 5, 6\\}$ with edges $0-1$, $1-2$, $1-4$, $1-6$, $2-3$, $3-4$, $4-5$, $5-6$.\\\n",
|
||||
"Define this graph in `networkx` and draw it."
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"id": "0cddf432",
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"### Give your answer in this cell. Add more cells if needed."
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "2e37a1e6",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"### Determine if $G_1$ is bipartite.\n",
|
||||
"If $G_1$ is bipartite, draw it in `networkx` with a two-colouring of the nodes. If not, explain why it is not bipartite."
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"id": "a6d6c25a",
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"### Give your answer in this cell. Add more cells if needed."
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "16b11144",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"## Q2: A Network of friends\n",
|
||||
" At a party with $n=6$ people, some people know each other\n",
|
||||
" already while others don't. Each of the 6 guests is asked how many\n",
|
||||
" friends they have at this party.\\\n",
|
||||
" One person says they know all of the others.\\\n",
|
||||
" One person says they know four of the others.\\\n",
|
||||
" Two report that they know three of the others. \\\n",
|
||||
" One person agrees they know two of the other guests, while\\\n",
|
||||
" one person says they know only one other.\n",
|
||||
" \n",
|
||||
"### Define a graph in `networkx` that represents this scenario.\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"id": "769c264d",
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"### Give your answer in this cell. Add more cells if needed."
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "f76aacf2",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"### Verify that the graph has the correct properties by displaying the diagonal of the square of the graphs adjacency matrix. \n",
|
||||
"\n",
|
||||
"_Hint_: `np.diag(X)` returns the entries on the main diagonal of $X$."
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"id": "e09a9ffe",
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"### Give your answer in this cell. Add more cells if needed."
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "8dccff32",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"## Q3: Isomorphic graphs"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "59339d77",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"In `networkx` we can check if two (smallish) graphs, $G$ and $H$, are **isomorphic** by using the `nx.is_isomorphic()` function: `nx.is_isomorphic(G,H)` evaluates as `True` if they are isomorphic.\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "82111bee",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"### Self-complementary cycle graph\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"Use `networkx` to check which of the cycle graphs $C_3$, $C_4$, $\\dots$, $C_{10}$ are isomorphic to its own complement.\\\n",
|
||||
"Notes:\n",
|
||||
"* You can use the constructor `nx.cycle_graph(n)` to make $C_n$\n",
|
||||
"* You can use the method `nx.complement(G)` to make construct the complement of the graph $G$.\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"id": "00b14230",
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"### Give your answer in this cell. Add more cells if needed. "
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "8e83a7ff",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"### Graphs that are isomorphic to their line graphs.\n",
|
||||
"\n",
|
||||
"Use `networkx` to check that all cycle graphs $C_3$, $C_4$, $\\dots$, $C_{10}$ are isomorphic to their line graphs.\n",
|
||||
"\n",
|
||||
"You can use the `nx.line_graph()` function."
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"id": "6506c686",
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"### Give your answer in this cell. Add more cells if needed. "
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "dd26ae6d",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"## Q4: Bipartite Graphs"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "73e51ef7",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"Consider the following affiliation network, $G_4$, with $8$ people labelled $a$ to $h$,\n",
|
||||
"and five foci (\"focal points\" of interaction) labelled $1$ to $5$: \n",
|
||||
"\n",
|
||||
"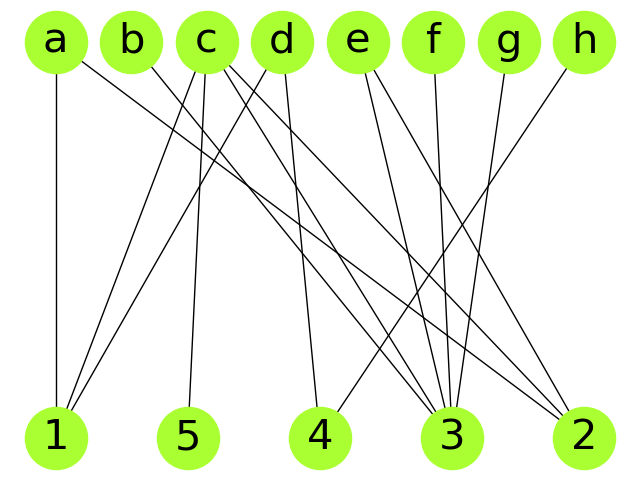\n",
|
||||
"\n",
|
||||
"1. Create this graph in `networkx` and draw it with a two-colouring.\n",
|
||||
"\n",
|
||||
"2. Compute the adjacency matrix of $G$.\n",
|
||||
"\n",
|
||||
"2. Draw the projection on (just) the people, in which two people are joined by an edge if they have a common\n",
|
||||
" focus. (You can do this by hand, or in `networkx`.)\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"id": "474fc87a",
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"# 1. Making and drawing the grap\n",
|
||||
"### Give your answer in this cell. Add more cells if needed. "
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"id": "da91f1bf",
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"# 2. Adjacency matrix\n",
|
||||
"### Give your answer in this cell. Add more cells if needed. "
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"id": "62aca129",
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"# 3. Compute and draw the projection\n",
|
||||
"### Give your answer in this cell. Add more cells if needed. "
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "4ea61c74",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"## Q5: Directed Graphs\n",
|
||||
"\n",
|
||||
"_For this question, the use of `networkx` is optional. You may write out your solution if you prefer._\n",
|
||||
"\n",
|
||||
"So far in CS4423 we have only considered **undirected graphs**. That is, the edge $a-b$ is the same as the edge $b-a$. \n",
|
||||
"\n",
|
||||
"Now I want you to think about *directed graphs* (also called _digraphs_): where the edge $a \\to b$ is not the same as the edge $b \\to a$. One can think of such edges as \"one way streets\": an edge that can be used to get from $a$ to $b$ can't be used to get from $b$ to $a$.\n",
|
||||
"\n",
|
||||
"There are numerous differences between directed and undirected graphs, including:\n",
|
||||
"* When you draw a digraph you add arrows to edges to indicate its direction.\n",
|
||||
"* If there is an edge $u \\to v$ and $v \\to u$, this can be represented by either having two edges between these nodes (with arrows in opposite directions), or by adding two arrows to a single edge.\n",
|
||||
"* The adjacency matrix is not necessarily symmetric.\n",
|
||||
"* The graph may have a path from node $u$ to node $v$, but not from $v$ to $u$.\n",
|
||||
"* We talk of a digraph being\n",
|
||||
" * **Strongly Connected** meaning there is a path between every pair of nodes\n",
|
||||
" * **Weakly Connected** meaning, for every pair of nodes, $u$ and $v$, there is a path from $u$ to $v$, or from $v$ to $u$.\n",
|
||||
" * **Disconnected** (same as the usual meaning of disconnected).\n",
|
||||
" * In `networkx` we construct a directed graph with the `nx.DiGraph()` constructor."
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "8e7973ee",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"Here is an example of a digraph in `networkx` which is strongly connected:"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"id": "a3302807",
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"G5a = nx.DiGraph([\"ab\", \"bc\", \"cd\", \"da\"]) \n",
|
||||
"nx.draw(G5a, **opts)"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "0d63ffc0",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"And here is one that is weakly connected: there is no path from $c$ to $a$, for example (since $d$ is a \"dead end\")."
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"id": "ce7cad10",
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"G5b = nx.DiGraph([\"ab\", \"bc\", \"cd\", \"ad\"])\n",
|
||||
"nx.draw(G5b, **opts)"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "04579b55",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"### Construct and draw a digraph\n",
|
||||
"\n",
|
||||
"Let $G_5$ be the directed graph on the nodes $0$, $1$, $2$, $3$, $4$ and $5$, with edges\n",
|
||||
"$0 \\to 1$, \n",
|
||||
"$1 \\to 2$, \n",
|
||||
"$1 \\to 3$, \n",
|
||||
"$1 \\to 4$, \n",
|
||||
"$1 \\to 5$, \n",
|
||||
"$2 \\to 4$, \n",
|
||||
"$3 \\to 2$, \n",
|
||||
"$3 \\to 4$, \n",
|
||||
"$4 \\to 3$, \n",
|
||||
"$5 \\to 0$ and $5 \\to 1$.\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"Either by hand, or in `networkx`, draw $G_5$. "
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"id": "c9344876",
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"## A drawing of the digraph\n",
|
||||
"### Give your answer in this cell. Add more cells if needed. "
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "35233bd6",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"### $G_5$ is not strongly connected.\n",
|
||||
"Show that this digraph is _not_ strongly connected (i.e., find a pair of nodes between which there is no path)."
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"id": "0a8eddd4",
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"### Give your answer in this cell. Add more cells if needed. "
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"id": "04d10b75",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"### Permuting the adjacency matrix.\n",
|
||||
"\n",
|
||||
"Suppose that $A$ is a the adjacency matrix of a digraph. Say there is a \n",
|
||||
"permutation matrix, $P$, such that \n",
|
||||
"$$ P^T A P = \\begin{pmatrix} X & Y \\\\ O & Z \\end{pmatrix}$$\n",
|
||||
"where $X$ and $Z$ are square matrices and $O$ is a zero matrix.\n",
|
||||
"\n",
|
||||
"Explain why, if there is such a $P$, the graph is not strongly connected.\n",
|
||||
"\n",
|
||||
"Write down the adjacency matrix for $G_5$, and also a permutation matrix $P$ such that $P^T A P$ has the structure described above. "
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"id": "b5ba1e67",
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"### Give your answer in this cell. Add more cells if needed. "
|
||||
]
|
||||
}
|
||||
],
|
||||
"metadata": {
|
||||
"kernelspec": {
|
||||
"display_name": "Python 3 (ipykernel)",
|
||||
"language": "python",
|
||||
"name": "python3"
|
||||
},
|
||||
"language_info": {
|
||||
"codemirror_mode": {
|
||||
"name": "ipython",
|
||||
"version": 3
|
||||
},
|
||||
"file_extension": ".py",
|
||||
"mimetype": "text/x-python",
|
||||
"name": "python",
|
||||
"nbconvert_exporter": "python",
|
||||
"pygments_lexer": "ipython3",
|
||||
"version": "3.13.1"
|
||||
},
|
||||
"toc": {
|
||||
"base_numbering": 1,
|
||||
"nav_menu": {},
|
||||
"number_sections": true,
|
||||
"sideBar": true,
|
||||
"skip_h1_title": true,
|
||||
"title_cell": "Table of Contents",
|
||||
"title_sidebar": "Contents",
|
||||
"toc_cell": true,
|
||||
"toc_position": {},
|
||||
"toc_section_display": true,
|
||||
"toc_window_display": false
|
||||
},
|
||||
"varInspector": {
|
||||
"cols": {
|
||||
"lenName": 16,
|
||||
"lenType": 16,
|
||||
"lenVar": 40
|
||||
},
|
||||
"kernels_config": {
|
||||
"python": {
|
||||
"delete_cmd_postfix": "",
|
||||
"delete_cmd_prefix": "del ",
|
||||
"library": "var_list.py",
|
||||
"varRefreshCmd": "print(var_dic_list())"
|
||||
},
|
||||
"r": {
|
||||
"delete_cmd_postfix": ") ",
|
||||
"delete_cmd_prefix": "rm(",
|
||||
"library": "var_list.r",
|
||||
"varRefreshCmd": "cat(var_dic_list()) "
|
||||
}
|
||||
},
|
||||
"types_to_exclude": [
|
||||
"module",
|
||||
"function",
|
||||
"builtin_function_or_method",
|
||||
"instance",
|
||||
"_Feature"
|
||||
],
|
||||
"window_display": false
|
||||
}
|
||||
},
|
||||
"nbformat": 4,
|
||||
"nbformat_minor": 5
|
||||
}
|
||||
Reference in New Issue
Block a user