diff --git a/year4/semester2/CS4423/assignments/assignment1/CS4423-Assignment-1.ipynb b/year4/semester2/CS4423/assignments/assignment1/CS4423-Assignment-1.ipynb
new file mode 100644
index 00000000..7f8849f2
--- /dev/null
+++ b/year4/semester2/CS4423/assignments/assignment1/CS4423-Assignment-1.ipynb
@@ -0,0 +1,503 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "id": "e4dd8d87",
+ "metadata": {
+ "toc": true
+ },
+ "source": [
+ "Table of Contents
\n",
+ ""
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "19989cc4",
+ "metadata": {},
+ "source": [
+ "# CS4423 Assignment 1: Solution Template\n",
+ "\n",
+ "This is a template for your solution to the `networkx` questions on Assignment 1. \n"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "4fc2a5c6",
+ "metadata": {},
+ "source": [
+ "### Collaboration Policy\n",
+ "\n",
+ "This is a homework assignment. You are welcome to collaborate with\n",
+ "class-mates if you wish. Please note:\n",
+ "* You may collaborate with at most two other people;\n",
+ "* Each of you must submit your own copy of your work;\n",
+ "* The file(s) you submit must contain a statement on the collaboration: who you collaborated with, and on what part of the assignment.\n",
+ "* The use of any AI tools, such as ChatGPT or DeepSeek is prohibited, and will be subject to disciplinary procedures. \n"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "a5bd0014",
+ "metadata": {},
+ "source": [
+ "### Instructions \n",
+ "\n",
+ "This assignment involves a mix of questions, some of which require use of the `networkx` Python module, and some which you solve by hand. You can decide the best way to submit your work (e.g., do everything in Jupyter, or a combination of hand-written work and\n",
+ "Jupyter notebook). However:\n",
+ "* Any file you submit must include your name and ID number.\n",
+ "* All files must be in PDF format. To convert your notebook to `pdf` the easiest method maybe to first export as 'html', then open that in a browser, and then print to pdf."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "eb8aa930",
+ "metadata": {},
+ "source": [
+ "### Preliminaries\n",
+ "\n",
+ "**Name:** Andrew Hayes\n",
+ "\n",
+ "**ID Number:** 213 \n",
+ "*Place your collaboration statement here*"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "50688c85",
+ "metadata": {},
+ "source": [
+ "### Usual list of Python modules"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "d548d182",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "import networkx as nx\n",
+ "import numpy as np\n",
+ "import matplotlib.pyplot as plt\n",
+ "opts = { \"with_labels\": True, \"node_color\": 'y' } # show labels; yellow noodes"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "6d7af8b8",
+ "metadata": {},
+ "source": [
+ "## Q1: Bipartite Graphs\n",
+ "\n",
+ "### Define and draw the following graph\n",
+ "Let $G_1$ be the graph on the nodes $\\{0, 1, 2, 3, 4, 5, 6\\}$ with edges $0-1$, $1-2$, $1-4$, $1-6$, $2-3$, $3-4$, $4-5$, $5-6$.\\\n",
+ "Define this graph in `networkx` and draw it."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "0cddf432",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "### Give your answer in this cell. Add more cells if needed."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "2e37a1e6",
+ "metadata": {},
+ "source": [
+ "### Determine if $G_1$ is bipartite.\n",
+ "If $G_1$ is bipartite, draw it in `networkx` with a two-colouring of the nodes. If not, explain why it is not bipartite."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "a6d6c25a",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "### Give your answer in this cell. Add more cells if needed."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "16b11144",
+ "metadata": {},
+ "source": [
+ "## Q2: A Network of friends\n",
+ " At a party with $n=6$ people, some people know each other\n",
+ " already while others don't. Each of the 6 guests is asked how many\n",
+ " friends they have at this party.\\\n",
+ " One person says they know all of the others.\\\n",
+ " One person says they know four of the others.\\\n",
+ " Two report that they know three of the others. \\\n",
+ " One person agrees they know two of the other guests, while\\\n",
+ " one person says they know only one other.\n",
+ " \n",
+ "### Define a graph in `networkx` that represents this scenario.\n"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "769c264d",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "### Give your answer in this cell. Add more cells if needed."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "f76aacf2",
+ "metadata": {},
+ "source": [
+ "### Verify that the graph has the correct properties by displaying the diagonal of the square of the graphs adjacency matrix. \n",
+ "\n",
+ "_Hint_: `np.diag(X)` returns the entries on the main diagonal of $X$."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "e09a9ffe",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "### Give your answer in this cell. Add more cells if needed."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "8dccff32",
+ "metadata": {},
+ "source": [
+ "## Q3: Isomorphic graphs"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "59339d77",
+ "metadata": {},
+ "source": [
+ "In `networkx` we can check if two (smallish) graphs, $G$ and $H$, are **isomorphic** by using the `nx.is_isomorphic()` function: `nx.is_isomorphic(G,H)` evaluates as `True` if they are isomorphic.\n"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "82111bee",
+ "metadata": {},
+ "source": [
+ "### Self-complementary cycle graph\n",
+ "\n",
+ "\n",
+ "Use `networkx` to check which of the cycle graphs $C_3$, $C_4$, $\\dots$, $C_{10}$ are isomorphic to its own complement.\\\n",
+ "Notes:\n",
+ "* You can use the constructor `nx.cycle_graph(n)` to make $C_n$\n",
+ "* You can use the method `nx.complement(G)` to make construct the complement of the graph $G$.\n"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "00b14230",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "### Give your answer in this cell. Add more cells if needed. "
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "8e83a7ff",
+ "metadata": {},
+ "source": [
+ "### Graphs that are isomorphic to their line graphs.\n",
+ "\n",
+ "Use `networkx` to check that all cycle graphs $C_3$, $C_4$, $\\dots$, $C_{10}$ are isomorphic to their line graphs.\n",
+ "\n",
+ "You can use the `nx.line_graph()` function."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "6506c686",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "### Give your answer in this cell. Add more cells if needed. "
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "dd26ae6d",
+ "metadata": {},
+ "source": [
+ "## Q4: Bipartite Graphs"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "73e51ef7",
+ "metadata": {},
+ "source": [
+ "Consider the following affiliation network, $G_4$, with $8$ people labelled $a$ to $h$,\n",
+ "and five foci (\"focal points\" of interaction) labelled $1$ to $5$: \n",
+ "\n",
+ "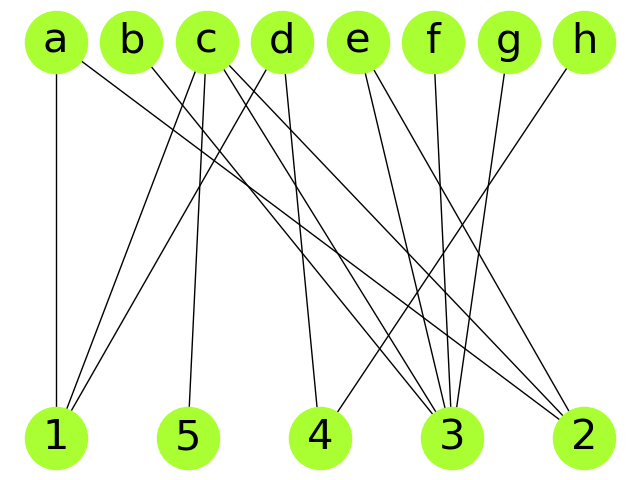\n",
+ "\n",
+ "1. Create this graph in `networkx` and draw it with a two-colouring.\n",
+ "\n",
+ "2. Compute the adjacency matrix of $G$.\n",
+ "\n",
+ "2. Draw the projection on (just) the people, in which two people are joined by an edge if they have a common\n",
+ " focus. (You can do this by hand, or in `networkx`.)\n"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "474fc87a",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "# 1. Making and drawing the grap\n",
+ "### Give your answer in this cell. Add more cells if needed. "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "da91f1bf",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "# 2. Adjacency matrix\n",
+ "### Give your answer in this cell. Add more cells if needed. "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "62aca129",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "# 3. Compute and draw the projection\n",
+ "### Give your answer in this cell. Add more cells if needed. "
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "4ea61c74",
+ "metadata": {},
+ "source": [
+ "## Q5: Directed Graphs\n",
+ "\n",
+ "_For this question, the use of `networkx` is optional. You may write out your solution if you prefer._\n",
+ "\n",
+ "So far in CS4423 we have only considered **undirected graphs**. That is, the edge $a-b$ is the same as the edge $b-a$. \n",
+ "\n",
+ "Now I want you to think about *directed graphs* (also called _digraphs_): where the edge $a \\to b$ is not the same as the edge $b \\to a$. One can think of such edges as \"one way streets\": an edge that can be used to get from $a$ to $b$ can't be used to get from $b$ to $a$.\n",
+ "\n",
+ "There are numerous differences between directed and undirected graphs, including:\n",
+ "* When you draw a digraph you add arrows to edges to indicate its direction.\n",
+ "* If there is an edge $u \\to v$ and $v \\to u$, this can be represented by either having two edges between these nodes (with arrows in opposite directions), or by adding two arrows to a single edge.\n",
+ "* The adjacency matrix is not necessarily symmetric.\n",
+ "* The graph may have a path from node $u$ to node $v$, but not from $v$ to $u$.\n",
+ "* We talk of a digraph being\n",
+ " * **Strongly Connected** meaning there is a path between every pair of nodes\n",
+ " * **Weakly Connected** meaning, for every pair of nodes, $u$ and $v$, there is a path from $u$ to $v$, or from $v$ to $u$.\n",
+ " * **Disconnected** (same as the usual meaning of disconnected).\n",
+ " * In `networkx` we construct a directed graph with the `nx.DiGraph()` constructor."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "8e7973ee",
+ "metadata": {},
+ "source": [
+ "Here is an example of a digraph in `networkx` which is strongly connected:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "a3302807",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "G5a = nx.DiGraph([\"ab\", \"bc\", \"cd\", \"da\"]) \n",
+ "nx.draw(G5a, **opts)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "0d63ffc0",
+ "metadata": {},
+ "source": [
+ "And here is one that is weakly connected: there is no path from $c$ to $a$, for example (since $d$ is a \"dead end\")."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "ce7cad10",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "G5b = nx.DiGraph([\"ab\", \"bc\", \"cd\", \"ad\"])\n",
+ "nx.draw(G5b, **opts)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "04579b55",
+ "metadata": {},
+ "source": [
+ "### Construct and draw a digraph\n",
+ "\n",
+ "Let $G_5$ be the directed graph on the nodes $0$, $1$, $2$, $3$, $4$ and $5$, with edges\n",
+ "$0 \\to 1$, \n",
+ "$1 \\to 2$, \n",
+ "$1 \\to 3$, \n",
+ "$1 \\to 4$, \n",
+ "$1 \\to 5$, \n",
+ "$2 \\to 4$, \n",
+ "$3 \\to 2$, \n",
+ "$3 \\to 4$, \n",
+ "$4 \\to 3$, \n",
+ "$5 \\to 0$ and $5 \\to 1$.\n",
+ "\n",
+ "\n",
+ "Either by hand, or in `networkx`, draw $G_5$. "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "c9344876",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "## A drawing of the digraph\n",
+ "### Give your answer in this cell. Add more cells if needed. "
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "35233bd6",
+ "metadata": {},
+ "source": [
+ "### $G_5$ is not strongly connected.\n",
+ "Show that this digraph is _not_ strongly connected (i.e., find a pair of nodes between which there is no path)."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "0a8eddd4",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "### Give your answer in this cell. Add more cells if needed. "
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "04d10b75",
+ "metadata": {},
+ "source": [
+ "### Permuting the adjacency matrix.\n",
+ "\n",
+ "Suppose that $A$ is a the adjacency matrix of a digraph. Say there is a \n",
+ "permutation matrix, $P$, such that \n",
+ "$$ P^T A P = \\begin{pmatrix} X & Y \\\\ O & Z \\end{pmatrix}$$\n",
+ "where $X$ and $Z$ are square matrices and $O$ is a zero matrix.\n",
+ "\n",
+ "Explain why, if there is such a $P$, the graph is not strongly connected.\n",
+ "\n",
+ "Write down the adjacency matrix for $G_5$, and also a permutation matrix $P$ such that $P^T A P$ has the structure described above. "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "b5ba1e67",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "### Give your answer in this cell. Add more cells if needed. "
+ ]
+ }
+ ],
+ "metadata": {
+ "kernelspec": {
+ "display_name": "Python 3 (ipykernel)",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.13.1"
+ },
+ "toc": {
+ "base_numbering": 1,
+ "nav_menu": {},
+ "number_sections": true,
+ "sideBar": true,
+ "skip_h1_title": true,
+ "title_cell": "Table of Contents",
+ "title_sidebar": "Contents",
+ "toc_cell": true,
+ "toc_position": {},
+ "toc_section_display": true,
+ "toc_window_display": false
+ },
+ "varInspector": {
+ "cols": {
+ "lenName": 16,
+ "lenType": 16,
+ "lenVar": 40
+ },
+ "kernels_config": {
+ "python": {
+ "delete_cmd_postfix": "",
+ "delete_cmd_prefix": "del ",
+ "library": "var_list.py",
+ "varRefreshCmd": "print(var_dic_list())"
+ },
+ "r": {
+ "delete_cmd_postfix": ") ",
+ "delete_cmd_prefix": "rm(",
+ "library": "var_list.r",
+ "varRefreshCmd": "cat(var_dic_list()) "
+ }
+ },
+ "types_to_exclude": [
+ "module",
+ "function",
+ "builtin_function_or_method",
+ "instance",
+ "_Feature"
+ ],
+ "window_display": false
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 5
+}