15 KiB
15 KiB
- #CT230 - Database Systems I
- Previous Topic: Query Processing: Relational Algebra
- Next Topic: File Organsiation
- Relevant Slides:
-
Trees
- What is a tree? #card
card-last-interval:: 14.2
card-repeats:: 3
card-ease-factor:: 2.7
card-next-schedule:: 2022-12-05T17:09:17.855Z
card-last-reviewed:: 2022-11-21T13:09:17.855Z
card-last-score:: 5
- A tree is a collection of data arranged as a finite set of elements called nodes, such that the tree is empty or the tree contains a distinguished node, called the root node, and all other nodes are arranged in subtrees such that each node has a parent node.
- Nodes typically contain data and some pointers to other nodes.
- Nodes may be: #card
card-last-interval:: -1
card-repeats:: 1
card-ease-factor:: 2.5
card-next-schedule:: 2022-11-15T00:00:00.000Z
card-last-reviewed:: 2022-11-14T16:15:58.945Z
card-last-score:: 1
- Root: No node points to it.
- Inner: Has parent & child nodes.
- Leaves: Has no child nodes.
- What is a binary tree? #card
card-last-interval:: 2.8
card-repeats:: 1
card-ease-factor:: 2.6
card-next-schedule:: 2022-11-17T11:23:05.626Z
card-last-reviewed:: 2022-11-14T16:23:05.627Z
card-last-score:: 5
- Tree data structures (a grouping of data) are used frequently in computing allowing data to be stored in a non-linear (non-list) way.
- They are often called binary trees where each node can have at most two child nodes.
-
SQL -> Relational Algebra
- How to translate SQL to Relational Algebra? #card
card-last-interval:: -1
card-repeats:: 1
card-ease-factor:: 2.5
card-next-schedule:: 2022-11-24T00:00:00.000Z
card-last-reviewed:: 2022-11-23T12:19:36.426Z
card-last-score:: 1
SELECTattributes corresponds to\pi.JOINs correspond to relational algebra joins\Joinwith ==any join conditions specified as part of the join.==- Any condition in a
WHEREclause corresponds to a sigma\sigmarelational algebra operator with associated conditions. - In addition, we have rules for aggregate functions (
SUM,AVG,COUNT, etc.),GROUP BY&HAVING, and subqueries.
- How to translate SQL to Relational Algebra? #card
card-last-interval:: -1
card-repeats:: 1
card-ease-factor:: 2.5
card-next-schedule:: 2022-11-24T00:00:00.000Z
card-last-reviewed:: 2022-11-23T12:19:36.426Z
card-last-score:: 1
-
Query Tree
- What is a query tree? #card
card-last-interval:: -1
card-repeats:: 1
card-ease-factor:: 2.5
card-next-schedule:: 2022-11-15T00:00:00.000Z
card-last-reviewed:: 2022-11-14T15:51:22.389Z
card-last-score:: 1
- A query tree is a binary tree that corresponds to a relational algebra expression where:
- (Input) Tables are the leaf nodes.
- Relational algebra operators are at internal nodes.
- (Output / Result) The root of the tree returns the result (often with one final relational algebra operator).
- The sequence of operations is directed from ^^leaves to root^^ and from ^^left to right^^.
- i.e., the bottom-most, left-most side of the tree is executed first.
- A query tree is a binary tree that corresponds to a relational algebra expression where:
-
Materialisation Evaluation #card
card-last-interval:: -1 card-repeats:: 1 card-ease-factor:: 2.5 card-next-schedule:: 2022-11-15T00:00:00.000Z card-last-reviewed:: 2022-11-14T20:24:42.937Z card-last-score:: 1- One approach to executing a query represented by a query tree is Materialisation Evaluation.
- Traverse the tree from bottom to top, left to right. At each stage:
-
- Execute internal node operation whenever data for its child nodes are available.
- Replace the internal node operation (and all child nodes) by the table resulting from executing the operation.
-
- Traverse the tree from bottom to top, left to right. At each stage:
- Note: The results of operations are saved as temporary tables and are used as inputs to other operators.
- One approach to executing a query represented by a query tree is Materialisation Evaluation.
-
How to Draw a Query Tree #card
card-last-interval:: -1 card-repeats:: 1 card-ease-factor:: 2.5 card-next-schedule:: 2022-11-19T00:00:00.000Z card-last-reviewed:: 2022-11-18T18:35:40.054Z card-last-score:: 1- We must remember the order of execution - from bottom to top, completing each level, and then left to right. Therefore:
- The first operations - fetching tables - should be at the leaves of the tree.
- The last operator - often
\pior aggregate functions - should be at the root of the tree. - Joins must be applied to tables (two at a time) and should be at internal nodes.
- Any other operators should be at one or more internal nodes.
- Important: When joining or multiplying more than two tables, operators can only be applied to two operands at a time.
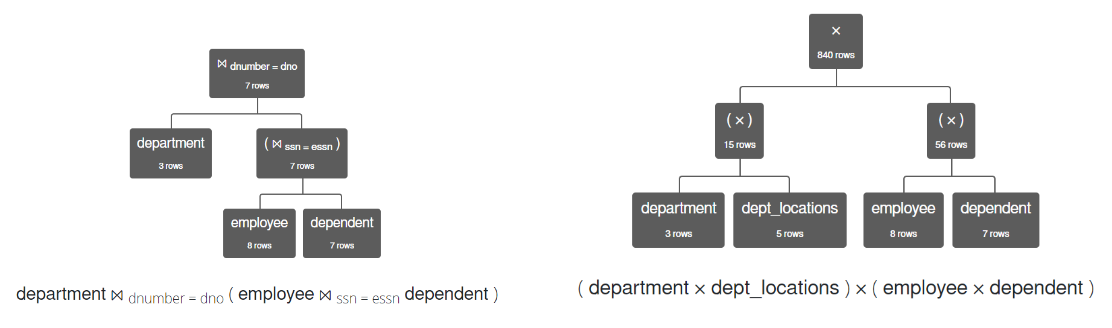
- We must remember the order of execution - from bottom to top, completing each level, and then left to right. Therefore:
-
Annotating Tree
- Each relational algebra operation can be evaluated using one of several different algorithms and Seach relational algebra expression can be evaluated in many ways.
- What is an evaluation plan? #card
card-last-interval:: -1
card-repeats:: 1
card-ease-factor:: 2.5
card-next-schedule:: 2022-11-15T00:00:00.000Z
card-last-reviewed:: 2022-11-14T15:52:56.044Z
card-last-score:: 1
- An evaluation plan is an annotated expression / query tree specifying the execution strategy for a query.
-
Issues to Consider with Query Trees #card
card-last-interval:: -1 card-repeats:: 1 card-ease-factor:: 2.5 card-next-schedule:: 2022-11-24T00:00:00.000Z card-last-reviewed:: 2022-11-23T12:19:19.197Z card-last-score:: 1- Size of temporary tables.
- Algorithms used for execution plan.
- What is a query tree? #card
card-last-interval:: -1
card-repeats:: 1
card-ease-factor:: 2.5
card-next-schedule:: 2022-11-15T00:00:00.000Z
card-last-reviewed:: 2022-11-14T15:51:22.389Z
card-last-score:: 1
- What is a tree? #card
card-last-interval:: 14.2
card-repeats:: 3
card-ease-factor:: 2.7
card-next-schedule:: 2022-12-05T17:09:17.855Z
card-last-reviewed:: 2022-11-21T13:09:17.855Z
card-last-score:: 5
-
Optimisation
- Different query trees for a given query can have different costs.
- Different evaluation plans for a given query can have different costs.
- Optimisation techniques attempt to choose the best among a number of potential query trees.
-
Cost Estimates
- How to calculate cost estimates? #card
card-last-interval:: -1
card-repeats:: 1
card-ease-factor:: 2.5
card-next-schedule:: 2022-11-22T00:00:00.000Z
card-last-reviewed:: 2022-11-21T13:05:07.723Z
card-last-score:: 1
- Cost factors include CPU speed, disk access time, network communication time, etc.
- Disk access is typically the predominant cost and can be measured by the number of blocks read / number of blocks written per query.
- What is the main cost estimate used? #card
card-last-interval:: -1
card-repeats:: 1
card-ease-factor:: 2.5
card-next-schedule:: 2022-11-15T00:00:00.000Z
card-last-reviewed:: 2022-11-14T15:52:39.027Z
card-last-score:: 1
- The main cost estimate used is the number of block transfers where each block contains a number of records.
- The number of blocks transferred from disk depends on:
- The size of the buffer in main memory - having more memory reduces the need for more disk accesses.
- Indexing structures used (primary, secondary, etc.).
- Whether or not all blocks of a file must be transferred.
- e.g., if a search can be done on the primary key of the index file or on the secondary index, then only retrieve blocks that satisfy the search condition.
- The number of blocks transferred from disk depends on:
- As in typical in Computing, often we use worst case estimates, knowing that any actual cost cannot exceed a worst case estimate.
- The main cost estimate used is the number of block transfers where each block contains a number of records.
-
DBMS Catalog #card
card-last-interval:: -1 card-repeats:: 1 card-ease-factor:: 2.5 card-next-schedule:: 2022-11-15T00:00:00.000Z card-last-reviewed:: 2022-11-14T20:24:53.519Z card-last-score:: 1- The DBMS Catalog stores ==statistical information about each table== such as table sizes, indexes & their depths, etc.
- The statistical information on the tables & attributes used in a query can be found in the DBMS catalog and these are used to calculate estimates also.
- In the DBMS catalog, for each table
R, information is stored on:- The number of tuples / records in
R. - The number of blocks containing tuples of table
R. - The size of a record in bytes.
- The blocking factor.
- Information on the number of distinct values per attribute and the number of values that would satisfy a set of equality operations on that attribute (by having averages, min, max, etc.).
- Information on indices (index type, index field values, etc.).
- The number of tuples / records in
- The DBMS Catalog stores ==statistical information about each table== such as table sizes, indexes & their depths, etc.
- How to calculate cost estimates? #card
card-last-interval:: -1
card-repeats:: 1
card-ease-factor:: 2.5
card-next-schedule:: 2022-11-22T00:00:00.000Z
card-last-reviewed:: 2022-11-21T13:05:07.723Z
card-last-score:: 1
-
Optimisation Approach 1: Compare Cost Estimates Across Different Solutions #card
card-last-interval:: -1 card-repeats:: 1 card-ease-factor:: 2.5 card-next-schedule:: 2022-11-15T00:00:00.000Z card-last-reviewed:: 2022-11-14T15:52:10.705Z card-last-score:: 1- Cost is usually measured as the total elapsed time for answering a query.
- One approach to optimisation is to calculate cost estimates for each possible query tree.
- The query tree with the lowest cost estimate should then be chosen.
-
Steps
-
- Generate query trees & evaluation plans (maybe not all).
- For each query tree, get cost estimates using the DBMS catalog.
- This results in a set of cost estimates such that the best can be chosen and the query tree with the lowest cost estimate can then be picked as the single best query tree & evaluation plan.
- Therefore, to choose among plans, the optimiser has to estimate the cost of each evaluation plan.
- There are two aspects to this. For each node of the tree, estimate the cost of performing associated operation, and estimate the size of the result and if it is sorted.
-
-
Summary
- While cost-based optimisation is good, it is expensive.
- As query complexity increases, so does the number of different query trees & plans possible, and each query tree requires its own cost estimates.
- NB: It is important that the amount of time an optimiser spends on calculating the best solution is not longer than the amount of time which would elapse if executing a solution picked at random.
-
Optimisation Approach 2: Heuristic Optimisation #card
card-last-interval:: -1 card-repeats:: 1 card-ease-factor:: 2.5 card-next-schedule:: 2022-11-15T00:00:00.000Z card-last-reviewed:: 2022-11-14T20:24:24.658Z card-last-score:: 1- Optimisers often use heuristics to reduce the number of choices that must be made in a cost-based fashion.
- Heuristic Optimisation transforms the query tree by ==using a set of rules that typically (but not always) improve execution performance.==
- Some cost-based estimation is also performed as part of the heuristic optimisation and to choose between a reduced set of trees and/or evaluation plans.
-
Steps
-
- Create a canonical query tree.
- Apply a set of heuristics to the tree to create a more efficient query tree.
- If appropriate, create cost estimates of this query tree to ensure the best evaluation plan.
-
-
Canonical Query Trees
- What is a canonical query tree? #card
card-last-interval:: -1
card-repeats:: 1
card-ease-factor:: 2.5
card-next-schedule:: 2022-11-15T00:00:00.000Z
card-last-reviewed:: 2022-11-14T16:22:12.535Z
card-last-score:: 1
- A canonical query tree is an inefficient query tree representing relational algebra expressions which can be created directly from the SQL solution following a sequence of quick & easy steps.
- A canonical query tree:
- Uses Cartesian Product instead of Joins.
- Keeps all conditions (
\sigma) together in one internal node. \pibecome the root node.
-
Steps to create a Canonical Query Tree with
SELECT/WHERE/FROMclauses and no sub-queries:-
- All relations in the
FROMclause become leaves of the tree.
- They should be combined with a Cartesian Product (
\times) of the relations.- Note: Only two relations can be involved in a Cartesian Product at a time (binary tree).
- All relations in the
-
- All conditions in the
WHEREclause and anyJOINconditions inWHEREorFROMclauses become a sequence of relational algebra in one inner node of the tree (with inputs from the previous step). - All conditions from the
SELECTclause become a relational algebra expression in the root node.
- All conditions in the
-
- What is a canonical query tree? #card
card-last-interval:: -1
card-repeats:: 1
card-ease-factor:: 2.5
card-next-schedule:: 2022-11-15T00:00:00.000Z
card-last-reviewed:: 2022-11-14T16:22:12.535Z
card-last-score:: 1
- Heuristic Optimisation must transform this canonical query tree into a final query tree that is efficient to execute.
- In general, heuristic optimisation tries to ==apply the most restrictive operators as early as possible== in the tree and to ==reduce the size of the temporary tables / results== created that move "up" the tree.
- Heuristic Optimisation must include rules for equivalence among relational algebra expressions that can be applied to the initial tree.
-
Heuristic Optimisation Algorithm #card
card-last-interval:: -1 card-repeats:: 1 card-ease-factor:: 2.5 card-next-schedule:: 2022-11-15T00:00:00.000Z card-last-reviewed:: 2022-11-14T16:25:04.590Z card-last-score:: 1- Input: A canonical query tree.
- Process:
-
- Decompose any
\sigmawith AND conditions into an individual\sigma. - Move each
\sigmaoperator as far down the query tree as possible, thus eliminating unwanted tuples.
- Heuristic 1 tries to reduce the size of the tables to be combined as much as possible.
- Therefore, if a selection operator (
\sigma) occurs after a Cartesian product or a join, check to see if it could occur before these operations.
- Therefore, if a selection operator (
- Decompose any
-
- Rearrange the leaf nodes so that the most restrictive
\sigmacan be applied first (using information from the DBMS catalog) and so that future JOINS are possible.
- Note: "Most restrictive" means those operators that result in relations with the fewest tuples or with the smallest absolute size.
- These operations should happen first, i.e., on the left-hand side of the lowest level of the tree.
- If we don't have any information from the DBMS catalog, we might leave nodes as they are, use the database schema (# of columns) to make a good estimate, or use sample data (# of rows) & database schema (# of columns) to make a good estimate.
- Rearrange the leaf nodes so that the most restrictive
-
- Combine Cartesian Product operators with
\sigmato form JOIN operators where appropriate (replacing all\times).
- Must first ensure that the leaf nodes are ordered such that this can occur. If not, re-order the leaf nodes and ensure to keep any select operators with the appropriate leaf node.
- Combine Cartesian Product operators with
-
- Decompose
\piand move each\pias far down the tree as possible, possibly creating new\pioperators in the process to eliminate unwanted columns.
- This heuristic ensure that the size of the tables to be joined are as small as possible.
- Therefore, for each
\picheck if that\pican be carried out before the join. For each table, check if additional $\pi$s can be introduced (these may not be stated explicitly in the query). - Note: Must ensure that all needed columns further up the tree are retained (even if they are not immediately necessary).
- Decompose
-
- Identify subtrees that represent groups of operations that can be executed by a single algorithm.
- Add an evaluation plan.
-
- Output: An efficient query tree.
