uni/year2/semester1/logseq-stuff/pages/Definitions & Planar Graphs.md

• #MA284 - Discrete Mathematics
• Previous Topic: Introduction to Graph Theory
• Next Topic: Convex Polyhedra
• Relevant Slides:

• Definitions

  • What is a walk? #card card-last-interval:: 2.8 card-repeats:: 2 card-ease-factor:: 2.6 card-next-schedule:: 2022-11-26T07:16:18.888Z card-last-reviewed:: 2022-11-23T12:16:18.890Z card-last-score:: 5
    • A walk is a sequence of vertices such that consecutive vertices are adjacent.
  • What is a trail? #card card-last-interval:: -1 card-repeats:: 1 card-ease-factor:: 2.5 card-next-schedule:: 2022-11-15T00:00:00.000Z card-last-reviewed:: 2022-11-14T16:14:59.935Z card-last-score:: 1
    • A trail is a walk in which no edge is repeated.
  • What is a path? #card card-last-interval:: 0.9 card-repeats:: 2 card-ease-factor:: 2.36 card-next-schedule:: 2022-11-15T17:22:40.523Z card-last-reviewed:: 2022-11-14T20:22:40.524Z card-last-score:: 3
    • A path is a trail in which no vertex is repeated, except possibly the first & last.
    • The path on n vertices is denoted P_n.

  • Example

    • {{renderer :mermaid_uiukfrr}} - ```mermaid flowchart LR B((B)) --- A((A)) B --- C((C)) C --- E((E)) E --- D((D)) B --- E --- A

      ```
      

      • (a,b,c,e,d) is a walk.
        • So too is (a,b,e,a,b,c) (not a trail or a path).
  • What is the length of a path? #card card-last-interval:: -1 card-repeats:: 1 card-ease-factor:: 2.5 card-next-schedule:: 2022-11-15T00:00:00.000Z card-last-reviewed:: 2022-11-14T20:22:48.413Z card-last-score:: 1
    • The length of a path is the number of edges in the sequence.

  • Cycles & Circuits

    • What is a cycle? #card card-last-interval:: -1 card-repeats:: 1 card-ease-factor:: 2.5 card-next-schedule:: 2022-11-15T00:00:00.000Z card-last-reviewed:: 2022-11-14T15:50:16.908Z card-last-score:: 1
      • A cycle is a path that begins & ends at the same vertex, but no other vertex is repeated.
      • A cycle on n vertices is denoted C_n.
    • What is a circuit? #card card-last-interval:: -1 card-repeats:: 1 card-ease-factor:: 2.5 card-next-schedule:: 2022-11-22T00:00:00.000Z card-last-reviewed:: 2022-11-21T13:05:28.290Z card-last-score:: 1
      • A circuit is a path that begins & ends at the same vertex, and no edge is repeated.
  • What does it mean if a graph is connected? #card card-last-interval:: 2.8 card-repeats:: 1 card-ease-factor:: 2.6 card-next-schedule:: 2022-11-17T11:16:09.571Z card-last-reviewed:: 2022-11-14T16:16:09.572Z card-last-score:: 5
    • A graph is connected if there is a path between every pair of vertices.
  • What is the degree of a vertex? #card card-last-interval:: 4 card-repeats:: 2 card-ease-factor:: 2.7 card-next-schedule:: 2022-11-25T13:10:12.122Z card-last-reviewed:: 2022-11-21T13:10:12.123Z card-last-score:: 5
    • The degree of a vertex is the number of edges emanating from it.
    • If v is a vertex, we denote its degree as d(v).

  • Handshaking Lemma

    • If we know the degree of every vertex in the graph, then we know the number of edges. This is the Handshaking Lemma.
    • What is the Handshaking Lemma? #card card-last-interval:: -1 card-repeats:: 1 card-ease-factor:: 2.5 card-next-schedule:: 2022-11-15T00:00:00.000Z card-last-reviewed:: 2022-11-14T15:54:11.744Z card-last-score:: 1
      • In any graph, the sum of the degrees of vertices in the graph, is always twice the number of edges.
        • \sum_{v \in V} d(v) = 2|E|

• Types of Graphs

  • What is a Complete Graph? #card card-last-interval:: 0.9 card-repeats:: 2 card-ease-factor:: 2.36 card-next-schedule:: 2022-11-15T17:23:00.989Z card-last-reviewed:: 2022-11-14T20:23:00.990Z card-last-score:: 3
    • A graph is complete if every pair of vertices is adjacent.
      • This family of graphs is very important.
    • Complete graphs are denoted K_n - the complete graph on n vertices.
  • What is a Bipartite Graph? #card card-last-interval:: 8.35 card-repeats:: 3 card-ease-factor:: 2.46 card-next-schedule:: 2022-11-29T21:09:36.899Z card-last-reviewed:: 2022-11-21T13:09:36.899Z card-last-score:: 5
    • A graph is bipartite if it is possible to partition the vertex set, V, into two disjoint sets, V_1 & V_2, such that there are no edges between any two vertices in the same set.
  • What is a Complete Bipartite graph? #card card-last-interval:: -1 card-repeats:: 1 card-ease-factor:: 2.5 card-next-schedule:: 2022-11-15T00:00:00.000Z card-last-reviewed:: 2022-11-14T15:51:45.394Z card-last-score:: 1
    • If a bipartite graph is such that every vertex in V_1 is connected to every vertex in V_2 (and vice versa), the graph is a complete bipartite graph.
    • If |V_1| = m and |V_2| = n, we denote it K_{m,n}.
  • What is a subgraph? #card card-last-interval:: 3.05 card-repeats:: 2 card-ease-factor:: 2.6 card-next-schedule:: 2022-11-17T21:23:07.436Z card-last-reviewed:: 2022-11-14T20:23:07.436Z card-last-score:: 5
    • We say that G_1 = (V_1, E_1) is a subgraph of G_2 = (V_2, E_2) provided V_1 \subset V_2 and E_1 \subset E_2.
  • What is an induced subgraph? #card card-last-interval:: -1 card-repeats:: 1 card-ease-factor:: 2.5 card-next-schedule:: 2022-11-23T00:00:00.000Z card-last-reviewed:: 2022-11-22T13:38:04.242Z card-last-score:: 1
    • We say that G_1(V_1, E_1) is an induced subgraph of G_2 = (V_2, E_2) provided that V_1 \subset V_2 and E_2 contains all edges of E_1 which join edges in V_1.

• Planar Graphs

  • What is a planar graph? #card card-last-interval:: -1 card-repeats:: 1 card-ease-factor:: 2.5 card-next-schedule:: 2022-11-15T00:00:00.000Z card-last-reviewed:: 2022-11-14T16:19:45.615Z card-last-score:: 1
    • If you can sketch a graph such that none of its edges cross, it is a planar graph.
  • What is a face? #card card-last-interval:: 0.98 card-repeats:: 1 card-ease-factor:: 2.36 card-next-schedule:: 2022-11-15T15:22:52.013Z card-last-reviewed:: 2022-11-14T16:22:52.013Z card-last-score:: 3
    • When a planar graph is drawn without edges crossing, the edges & vertices of the graph divide the plane into regions called faces.
    • The number of faces does not change no matter how you draw the graph, as long as no edges cross.

  • Example

    • The graph K_{2,3} is planar. background-color:: red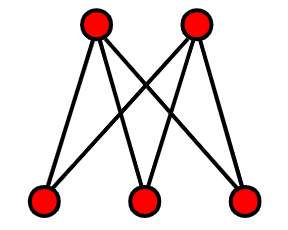
      • 
      • draws/2022-10-28-11-04-05.excalidraw
      • The planar representation K_{2,3} has 3 faces (the "outside" region counts as a face).
    • Give a planar representation of K_4, and count how many faces it has. background-color:: red
      • draws/2022-10-28-11-22-12.excalidraw
    • Why "face"? background-color:: red
      • draws/2022-10-28-11-25-20.excalidraw

• Euler's Formula for Planar Graphs #card

  card-last-interval:: -1 card-repeats:: 1 card-ease-factor:: 2.5 card-next-schedule:: 2022-11-15T00:00:00.000Z card-last-reviewed:: 2022-11-14T16:18:07.821Z card-last-score:: 1
  • For any ^^(connected) planar graph^^ with v vertices, e edges, and f faces, we have:
    • v - e + f = 2

  • Outline of Proof

    • Start with P_2.
      • Here, v=2, e = 1, f=1. So v-e+f=2.
      • Any other graph can be made by adding vertices & edges (or just edges) to P_2.
    • Suppose v-e+f=2 for a graph.
      • If we add a new edge with a new vertex, then no new face is created, so v-e+f does not change.
      • If we add a new edge without a new vertex, then f will increase by 1, so again, v-e+f does not change.

  • Example

    • Is it possible for a connected planar graph to have 5 vertices, 7 edges, and 3 faces? Explain. background-color:: red
      • No. Euler's formula tells us that v-e+f=2.
        • Here, v=5, e=7, f=3, so v-e+f=1.
      • Any such graph is not planar.