uni/year2/semester1/logseq-stuff/pages/Block Ciphers & Stream Ciphers.md

• #CT255 - Next Generation Technologies II
• Previous Topic: DIffie-Hellman Key Exchange
• Next Topic: Message Authentication
• Relevant Slides:

• Block Ciphers

  • Encryption Algorithms Based on Block Ciphers

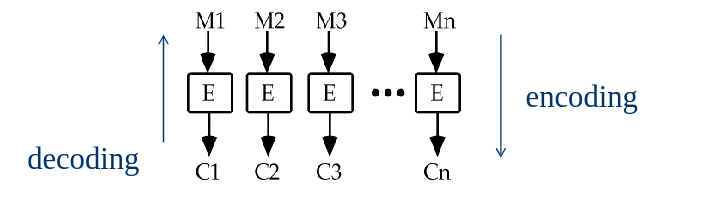
    collapsed:: true
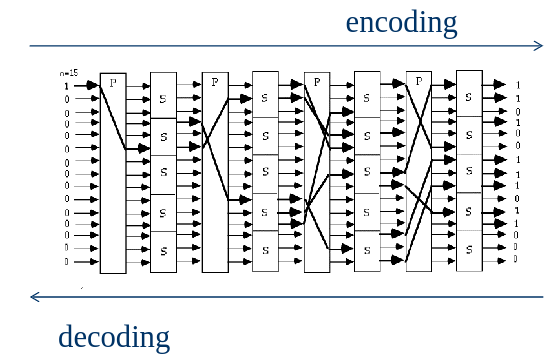
    • In a block cipher, the message is broken into blocks M1, M2, etc., of K bits length, each of which is then encrypted.
      • 
      • Most ciphers that we saw before process blocks of just one character.
    • Claude Shannon suggested to use the two primitive cryptographic operations as building blocks for such ciphers:
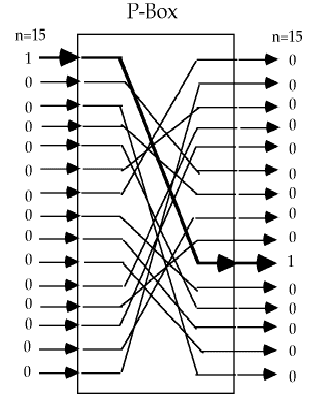
      • Substitution.
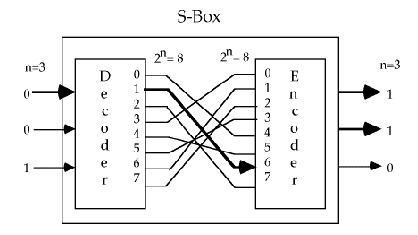
      • Permutation.

    • The Permutation Operation

      • A binary word (i.e., block) has its bits re-ordered (permuted).
        • The re-ordering forms the key.
        • The Operation is represented by a P-box.
      • 
        • The example allows for 15! combinations.
        • The key describes the combinations used.

    • The Substitution Operation

      • A binary word is replaced by another binary word.
      • The whole substitution function forms the key.
      • The operation is represented by an S-box.
      • The box below allows for 8! combinations.
        • 
      • The key describes the combination used.

    • Substitution-Permutation Network

      • The key describes the internal wiring of all S-boxes & P-boxes.
        • The same key can be used for encoding & decoding, hence it is a private key encryption algorithm.
      • The direction of the process determines encoding / decoding.
      • 

  • Confusion & Diffusion

    • A cipher needs to completely obscure the statistical properties of the original message.
    • Shannon introduced two terms to describe this:
      • Diffusion seeks to make the statistical relationship between the plaintext & ciphertext as complex as possible.
      • Confusion seeks to make the relationship between the statistics of the ciphertext and the value of the encryption key as complex as possible.
    • Both thwart attempts to deduce the key used via a cryptanalysis.

  • Reversible Transformation

    • An important block cipher principle is Reversible Transformation - transformations must be reversible or non-singular.
    • There must be a 1:1 association between an $n$-bit plaintext and an $n$-bit ciphertext, otherwise mapping is irreversible.

  • Features of Private-Key Cryptography

    • Traditional private/secret/single key cryptography uses one key, shared by only the sender and the receiver.
    • The algorithm/cipher itself is public, i.e., not a secret.
    • If the key is disclosed, communications are compromised.
    • The key is also symettric, parties are equal.
      • Hence, methods doe do not protect the sender from receiver forging .
    • Examples include DES and AES.

  • AES

    • The Advanced Encryption Standard (AES) is the successor of DES.
    • It is a modern block cipher with 128 bits block length.
    • Uses 128, 192, or 256 bit long keys.
    • The de-facto standard for secure encryption.
    • Widely used for file/data encryption, and secure network communication.

  • Why does Block & Key length matter?

    • Cryptographic algorithms with short block length can be tackled easily.
    • Large keys & long blocks prevent brute force attacks
    • The DES cipher used 56-bit keys - The generally accepted minimum key length today is 128-bit.

    • Brute Force Attacks

      • Always possible to simply try every key.
      • Most basic attack, effort proportional to key size.
      • Assume that you either know or recognise plaintext.

  • The Feistel Cipher

    • In practice, we need to be able to decrypt messages as well as encrypt them. Hence we either need to define inverses for each of the S & P-boxes (but this doubles the code / hardware needed) or define a structure that is easy to reverse, so you can use basically the same code or hardware for both encryption & decryption.
    • A Feistel Cipher is such a structure that is easy to reverse.
      • It is based on the concept of the invertible product cipher.
      • Most symmetric block ciphers are based on a Feistel Cipher structure.
    • Feistel invented a suitable structure which adapted Shannon's S-P network into an easily invertible structure.
      • Essentially, the same hardware or software is used for both encryption & decryption, with just a slight change in how the keys are used.

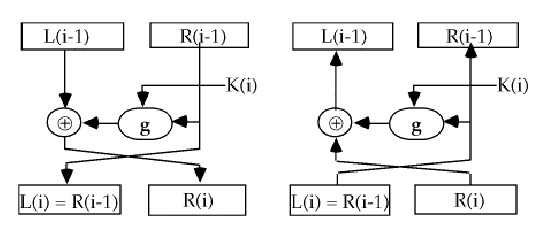
    • A Single Round

      collapsed:: true
      • The idea is to partition the input block into two halves, L(i-1) & R(i-1), and use only R(i-1) in the i^{\text{th}} round (part) of the cipher.
      • The function g incorporates one stage of the S-P network, controlled by part of the key K(i) known as the i^{\text{th}} subkey.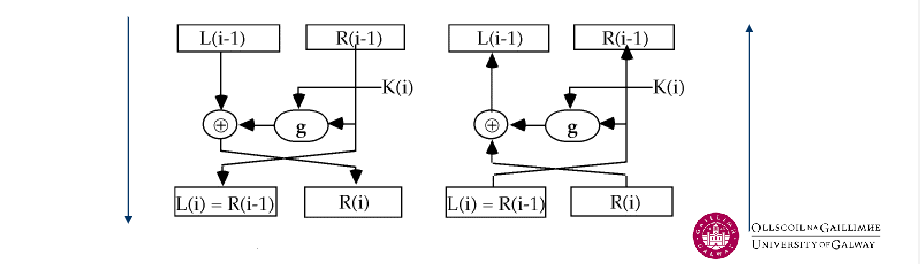
      • 
      • A round of a Feistel Cipher can be described functionally as:
        • L(i) = R(i-1)
        • R(i) = L(i-1) \text{ EXOR } g(K(i), R(i-1))
        • 

    • A Feistel Network

      • Perform multiple transformation (single rounds) sequentially, whereby the output of the $i$^{th} round becomes the input of the $(i+1)$^{th} round.
      • Every round gets its own subkey, which is derived from the master key.
      • The decryption process goes from bottom to top.

    • Feistel Cipher Design Elements

      • Block size.
      • Key size.
      • Number of rounds.
      • Subkey generation algorithm.
      • Round function.
      • Fast software encryption / decryption.