Table of Contents
- -CS4423 - Networks¶
Niall Madden,
-School of Mathematical and Statistical Sciences
-University of Galway
(These notes are adapted from Angela Carnecale's work)
-This notebook is at: https://www.niallmadden.ie/2425-CS4423/W01/CS4423-W01-2.ipynb
-Week 1, Lecture 2:¶
Graphs and networkx¶
-import networkx as nx
-News¶
-
-
- Still working on confirming the lab times. We'll certainly have a lab session, Wednesday at 10am in CA116a. -
Tuesday at 4 in AC215 is suboptimal... let's see if we can improve on that...
-After that, we'll review some of the slides I didn't cover on Wednesday (see https://universityofgalway.instructure.com/courses/31889/files?preview=2325934)
-Graphs¶
A graph can serve as a mathematical model of a network.
-Later, we will use the networkx package to work with examples of graphs and networks.
This notebook gives an introduction into graph theory, along with some basic, useful
-networkx commands.
An example: the Internet (circa 1970)¶
-Example. The internet (more precisely, ARPANET) in December 1970. Nodes are computers, -connected by a link if they can directly communicate with each other. -At the time, only 13 computers participated in that network.
-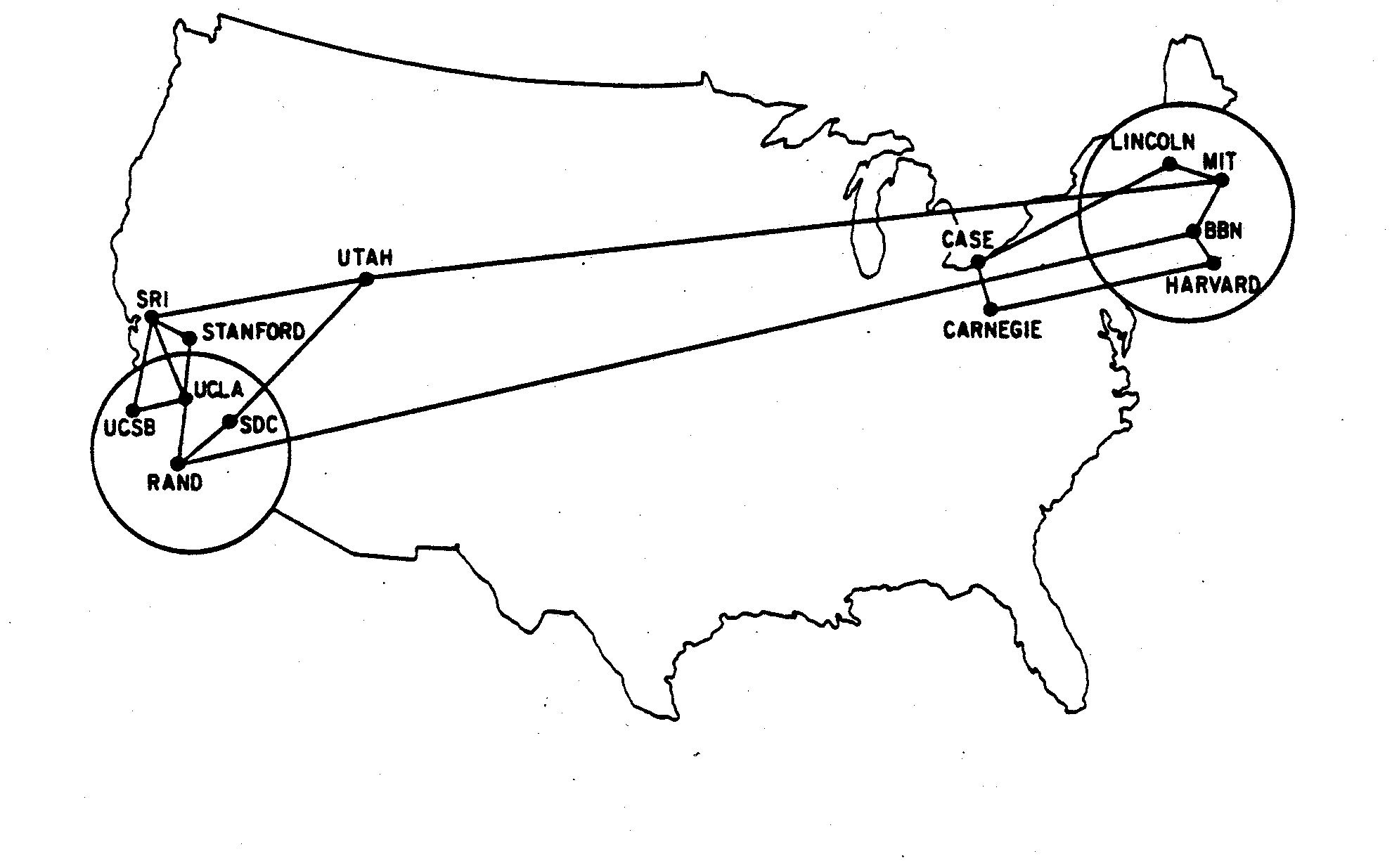
!cat ../data/arpa.adj
-UCSB SRI UCLA -SRI UCLA STAN UTAH -UCLA STAN RAND -UTAH SDC MIT -RAND SDC BBN -MIT BBN LINC -BBN HARV -LINC CASE -HARV CARN -CASE CARN --
The very first ARPANET network was even smaller, with node 1 being UCLA and node 2 being SRI. The first ever message was sent on 29 October 1969. The intended message was "Login" but things didn't quite work and the computers crashed just after the more prophetic message "Lo" was displayed...
-The following diagram, built from the adjacencies in the list, -contains the same information, without the distracting details of the -US geography! (This is actually an important point: networks reflect only the topology of the object being studied). Also - don't worry about the syntax: we'll come back to that later!
-H = nx.read_adjlist("../data/arpa.adj")
-opts = { "with_labels": True, "node_color": 'y' }
-nx.draw(H, **opts)
-Simple Graphs¶
Definition. A (simple) graph -is a pair $G = (X, E)$, consisting of a (finite) set $X$ of -objects, called nodes or vertices or points, -and $E$ is the of links or edges; every edge is a set consisting of two different vertices.
-We can also write $E \subseteq \binom{X}{2}$, where $\binom{X}{2}$, pronounced as "$X$ choose 2", is the set of all $2$-element subsets of $X$.
-Usually, $n$ is used to denote the number of vertices of a graph, -$n = |X|$, -and $m$ for the number of edges, $m = |E|$.
-$n = |X|$ is called the order of the graph $G$, and $m = |E|$ is called the size of $G$.
-The notation $\binom{X}{2}$ for the set of all $2$-element subsets of $X$ is -motivated by the fact that if $X$ has $n$ elements then -$\binom{X}{2}$ has $\binom{n}{2} = \frac{1}{2} n(n-1)$ elements: -$$\left|\binom{X}{2}\right| = \binom{|X|}{2}.$$ -Obviously, $m \leq \binom{n}{2}$.
-Example.
-$G=(X,E)$ with $X = \{ A, B, C, D \}$ and $E = \{ \{AB\}, \{BC\}, \{BD\}, \{CD\} \}$. -Notation: usually we'll be a bit lazy and write $\{ A, B \}$) as just $AB$. So $E = \{ AB, BC, BD, CD \}$.
-So $G$ is a graph of order $4$ and size $4$.
-G = nx.Graph()
-G.add_edges_from([('A', 'B'), ('B', 'C'), ('B', 'D'), ('C', 'D')])
-nx.draw(G, **opts)
-import networkx as nx
-opts = { "with_labels": True, "node_color": 'y' } # show labels
-Making a graph:¶
In networkx, we can construct this graph with the Graph constructor function, which takes the
-node and edge sets $X$ and $E$ in a variety of formats.
The simplest approach is to use $2$-letter strings for the edges: this implicitly defines the nodes too.
-Here is our graph from earlier:
-G = nx.Graph(["AB", "BC", "BD", "CD"])
-G
-<networkx.classes.graph.Graph at 0x7f519c817560>-
-
-
- The
pythonobjectGrepresenting the graph $G$ has lots of useful attributes. Firstly, it hasnodesandedges.
-
G.nodes
-NodeView(('A', 'B', 'C', 'D'))
-list(G.nodes)
-['A', 'B', 'C', 'D']-
G.edges
-EdgeView([('A', 'B'), ('B', 'C'), ('B', 'D'), ('C', 'D')])
-list(G.edges)
-[('A', 'B'), ('B', 'C'), ('B', 'D'), ('C', 'D')]
-A loop over a graph G will effectively loop over G's nodes. As an example, (recall?) that the degree of a node is the number of edges incident to it (or, if you prefer, the number of neighbours).
for node in G:
- print(f"node {node} has degree {G.degree(node)}")
-node A has degree 1 -node B has degree 3 -node C has degree 2 -node D has degree 2 --
We can count the nodes, and the edges.
-G.number_of_nodes()
-4-
G.order()
-4-
G.number_of_edges()
-4-
G.size()
-4-
To draw the graph:
-nx.draw(G, **opts)
-The example also illustrates a typical way how diagrams of graphs are drawn: -nodes are represented by small circles, and edges by lines connecting the nodes.
-Adding and removing nodes and edges¶
A graph G can be modified, by adding nodes one at a time ...
G.add_node(1)
-list(G.nodes)
-nx.draw(G, **opts)
-or many nodes at once ...
-G.add_nodes_from([2, 3, 5])
-list(G.nodes)
-nx.draw(G, **opts)
--
-
- ... or even as nodes of another graph
H
-
G.add_nodes_from(H)
-list(G.nodes)
-['A', - 'B', - 'C', - 'D', - 1, - 2, - 3, - 5, - 'UCSB', - 'SRI', - 'UCLA', - 'STAN', - 'UTAH', - 'RAND', - 'SDC', - 'MIT', - 'BBN', - 'LINC', - 'HARV', - 'CASE', - 'CARN']-
G.order(), G.size()
-(21, 4)-
Adding edges works in a similar fashion
-G=nx.Graph( ["AB", "BC", "BD", "DC"] )
-G.add_edge(1,2)
-list(G.edges)
-nx.draw(G, **opts)
-#edge = (2,3)
-#G.add_edge(*edge)
-#list(G.edges)
-Add edges from a list:
-G.add_edges_from([(1,5), (2,5), (3,5)])
-list(G.edges)
-[('A', 'B'),
- ('B', 'C'),
- ('B', 'D'),
- ('C', 'D'),
- (1, 2),
- (1, 5),
- (2, 5),
- (5, 3)]
-Add edges from another graph:
-G.add_edges_from(H.edges)
-list(G.edges)
-[('A', 'B'),
- ('B', 'C'),
- ('B', 'D'),
- ('C', 'D'),
- (1, 2),
- (1, 5),
- (2, 5),
- (5, 3),
- ('UCSB', 'SRI'),
- ('UCSB', 'UCLA'),
- ('SRI', 'UCLA'),
- ('SRI', 'STAN'),
- ('SRI', 'UTAH'),
- ('UCLA', 'STAN'),
- ('UCLA', 'RAND'),
- ('UTAH', 'SDC'),
- ('UTAH', 'MIT'),
- ('RAND', 'SDC'),
- ('RAND', 'BBN'),
- ('MIT', 'BBN'),
- ('MIT', 'LINC'),
- ('BBN', 'HARV'),
- ('LINC', 'CASE'),
- ('HARV', 'CARN'),
- ('CASE', 'CARN')]
-nx.draw(G, **opts)
-There are corresponding commands for removing nodes or edges from a graph G
G.order(), G.size()
-(21, 25)-
G.remove_edge(3,5)
-G.order(), G.size()
-(21, 24)-
G.remove_edges_from(H.edges())
-
-G.order(), G.size()
-(21, 7)-
nx.draw(G, **opts)
-G.remove_nodes_from(H)
-nx.draw(G, **opts)
--
-
- Removing a node will silently delete all edges it forms part of -
G.remove_nodes_from([1, 2, 3, 5])
-G.order(), G.size()
-(4, 4)-
nx.draw(G, **opts)
-That is, networkx is ensuring what we get is a proper graph, which is a subgraph of the original one.
Subgraphs and Induced subgraphs¶
Given $G=(X,E)$, a subgraph of $G$ is $H=(Y,E_H)$ with $Y\subseteq X$ and $E_H\subseteq E\cap \binom{Y}{2}$.
-So, all the nodes in $H$ are also in $G$. And any edge in $H$ was also in $G$, and is incident only to vertices in $Y$.
-One of the most important subgraphs of $G$ is the induced subgraph on $Y\subseteq X$ is the graph $H=\left(Y,E\cap \binom{Y}{2}\right)$. That is, given a subset $Y$ of $X$, we include all possible edges from $G$ too.
--
-
- Each node has a list of neighbours, the nodes it is -directly connected to by an edge of the graph. -
list(G.neighbors('B'))
-['A', 'C', 'D']-
G['B']
-AtlasView({'A': {}, 'C': {}, 'D': {}})
-list(G['B'])
-['A', 'C', 'D']-
As mentioned earlier, the number of neighbours of a node $x$ is its degree
-G.degree('B')
-3-
G.degree
-DegreeView({'A': 1, 'B': 3, 'C': 2, 'D': 2})
-list(G.degree)
-[('A', 1), ('B', 3), ('C', 2), ('D', 2)]
-Anybody knows/remembers a fundamental relationship between (the sum of) the degrees and the size of a graph?
-Important Graphs¶
-Complete Graphs¶
The complete graph -on a vertex set $X$ is the graph with edge set all of $\binom{X}{2}$. E.g., if $X=\{0,1,2,3\}$, then $E=\{01, 02, 03, 12, 13, 23\}$.
-nodes = range(4)
-list(nodes)
-[0, 1, 2, 3]-
E4 = [(x, y) for x in nodes for y in nodes if x < y]
-print(E4)
-[(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)] --
K4 = nx.Graph(E4)
-nx.draw(K4)
-While it is somewhat straightforward to find all $2$-element
-subsets of a given set $X$ with a short python program,
-it is probably more convenient (and possibly efficient) to use a function from the
-itertools package for this purpose.
from itertools import combinations
-nodes5 = range(5)
-combinations(nodes5, 2)
-<itertools.combinations at 0x7f5194447380>-
print(list(combinations(nodes5, 2)))
-[(0, 1), (0, 2), (0, 3), (0, 4), (1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)] --
K5 = nx.Graph(combinations(nodes5, 2))
-nx.draw(K5, **opts)
-We can turn this procedure into a python function that
-constructs the complete graph for an arbitrary vertex set $X$.
def complete_graph(nodes):
- return nx.Graph(combinations(nodes, 2))
-nx.draw(complete_graph(range(3)), **opts)
-nx.draw(complete_graph(range(4)), **opts)
-nx.draw(complete_graph(range(5)), **opts)
-nx.draw(complete_graph(range(6)), **opts)
-nx.draw(complete_graph("ABCD"), **opts)
-In fact, networkx has its own implementation of complete graphs.
nx.draw(nx.complete_graph("NETWORKS"), **opts)
-Petersen Graph¶
The Petersen Graph -is a graph on $10$ vertices with $15$ edges.
-It can be constructed -as the complement of the line graph of the complete graph $K_5$, -i.e., -as the graph with vertex set -$$X = \binom{\{0,1,2,3,4\}}{2}$$ (the edge set of $K_5$) and -with an edge between $x, y \in X$ whenever $x \cap y = \emptyset$.
-nx.draw(K5, **opts)
-lines = K5.edges
-print(list(lines))
-[(0, 1), (0, 2), (0, 3), (0, 4), (1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)] --
print(list(combinations(lines, 2)))
-[((0, 1), (0, 2)), ((0, 1), (0, 3)), ((0, 1), (0, 4)), ((0, 1), (1, 2)), ((0, 1), (1, 3)), ((0, 1), (1, 4)), ((0, 1), (2, 3)), ((0, 1), (2, 4)), ((0, 1), (3, 4)), ((0, 2), (0, 3)), ((0, 2), (0, 4)), ((0, 2), (1, 2)), ((0, 2), (1, 3)), ((0, 2), (1, 4)), ((0, 2), (2, 3)), ((0, 2), (2, 4)), ((0, 2), (3, 4)), ((0, 3), (0, 4)), ((0, 3), (1, 2)), ((0, 3), (1, 3)), ((0, 3), (1, 4)), ((0, 3), (2, 3)), ((0, 3), (2, 4)), ((0, 3), (3, 4)), ((0, 4), (1, 2)), ((0, 4), (1, 3)), ((0, 4), (1, 4)), ((0, 4), (2, 3)), ((0, 4), (2, 4)), ((0, 4), (3, 4)), ((1, 2), (1, 3)), ((1, 2), (1, 4)), ((1, 2), (2, 3)), ((1, 2), (2, 4)), ((1, 2), (3, 4)), ((1, 3), (1, 4)), ((1, 3), (2, 3)), ((1, 3), (2, 4)), ((1, 3), (3, 4)), ((1, 4), (2, 3)), ((1, 4), (2, 4)), ((1, 4), (3, 4)), ((2, 3), (2, 4)), ((2, 3), (3, 4)), ((2, 4), (3, 4))] --
edges = [e for e in combinations(lines, 2)
- if not set(e[0]) & set(e[1])]
-len(edges)
-15-
P = nx.Graph(edges)
-nx.draw(P, **opts)
-Even though there is no parameter involved in this example,
-it might be worth wrapping the construction up into a python
-function.
def petersen_graph():
- nodes = combinations(range(5), 2)
- G = nx.Graph()
- for e in combinations(nodes, 2):
- if not set(e[0]) & set(e[1]):
- G.add_edge(*e)
- return G
-nx.draw(petersen_graph(), **opts)
-Code Corner¶
-python¶
--
-
- list unpacking operator
*e: ifeis a list, an -argument*epasses the elements ofeas individual arguments -to a function call.
-
-
-
- dictionary unpacking operator
**opts:pythonfunction calls take positional arguments and keyword arguments. The keyword arguments can be collected in a dictionaryopts(with the keywords as keys). This dictionary can then be passed into the function call in its "unwrapped" form**opts.
-
-
-
- set intersection: if
aandbare sets thena & brepresents the intersection ofaandb. In a boolean context, an empty set counts asFalse, and a non-empty set asTrue.
-
a = set([1,2,3])
-b = set([3,4,5])
-a & b
-{3}
-bool({}), bool({3})
-(False, True)-
-
-
list[doc] turns its argument into apythonlist (if possible).
-
list("networks")
-['n', 'e', 't', 'w', 'o', 'r', 'k', 's']-
-
-
- list comprehension [doc] allows the construction of new list from old ones
-without explicit
forloops (orifstatements).
-
[(x, y) for x in range(4) for y in range(4) if x < y]
-[(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)]-
networkx¶
--
-
- the
read_adjlistcommand [doc] constructs a graph from a text file inadjformat.
-
-
-
Graphconstructor and applicable methods [doc]: ifGisGraphobject then-
-
G.nodesreturns the nodes of a graphG(as an iterator),
-G.edgesreturns the edges of a graphG(as an iterator),
-- ... -
-
-
-
complete_graph[doc]
-
itertools¶
--
-
combinations[doc] returns the $k$-element combinations of a given list (as an iterator).
-
print(["".join(c) for c in combinations("networks", 2)])
-['ne', 'nt', 'nw', 'no', 'nr', 'nk', 'ns', 'et', 'ew', 'eo', 'er', 'ek', 'es', 'tw', 'to', 'tr', 'tk', 'ts', 'wo', 'wr', 'wk', 'ws', 'or', 'ok', 'os', 'rk', 'rs', 'ks'] --
-